«Алгоритмы сортировки массивов». Метод Пузырька. Алгоритм Хоара. Слияния. VBA EXCEL
Для удобства рассматриваю пример на языке - VBA, приложение EXCEL.
- Задачи сортировки массивов данных
- Метод Пузырька или пузырьковая сортировка
- Алгоритм Хоара или быстрая, рекурсивная сортировка
- Сортировка Слиянием и Хоара - совмещение
Задачи сортировки массивов данных
Приложение позволяет сравнить скорость выполнения разных вариантов сортировки…
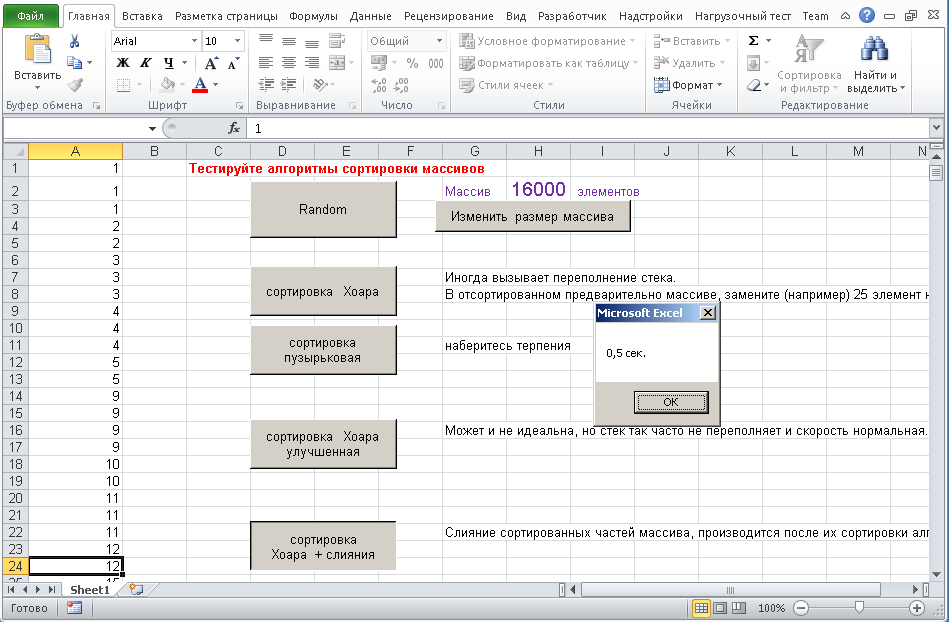
Рис.1 Алгоритмы сортировки массивов.VBA.Макросы.
В моем массиве хранятся (генерируются случайным образом) только целые числа.
Массив глобальный, т.е. все подпрограммы имеют к нему доступ.
Public a( ) As Integer
Размер массива пользователь может изменять (в пределах от 300 до 32000).
После окончания сортировки появляется сообщение о длительности процесса работы по таймеру.
Поскольку сортировка массива подразумевает замену элементов местами, то без процедуры (подпрограммы) swap здесь не обойтись.
Нет, обойтись, конечно, можно, но придется часто повторять однотипный код из трех операторов.
Итак, замена значений переменных с использованием третьей (временной):
Private Sub swap(p As Integer, q As Integer, bool As Boolean)
'меняет местами два элемента массива
Dim t As Integer
t = a(p): a(p) = a(q): a(q) = t
bool = False
End Sub
В процедуру передаются два индекса элементов массива и логическая переменная (по ссылке),
которую я буду называть «показатель сортировки» или «флаг сортировки».
При любом вызове этой процедуры, как видите, флаг сбрасывается.
Метод Пузырька или пузырьковая сортировка
наиболее простой и не очень быстрый метод. Есть смысл использовать его для небольших массивов и в учебных целях.
Его суть: сравнить два соседних элемента массива и если они расположены не в «нужном» порядке, то поменять их местами.
Вот условие сортировки по возрастанию:
If a(i) > a(i + 1) Then swap i, i + 1, bool
А вот по убыванию:
If a(i) < a(i + 1) Then swap i, i + 1, bool
Показал и все. В дальнейшем сортирую только по возрастанию. Для удобства восприятия
Как видите, если соседние элементы равны или не удовлетворяют условию замены, то просто ничего не происходит,
а элементы остаются на своих местах.
Следующий момент: соседние элементы, конечно, рассматриваются и сравниваются парами в цикле. Но можно цикл начать от начала массива (прямой прогон), а можно с конца (обратный прогон).
Вот, прямой прогон:
For i = 1 To sizeArr -1 'прямой ход.
If a(i) > a(i + 1) Then swap i, i + 1, bool
Next i
А вот, обратный прогон:
For i = sizeArr To 2 Step -1 'обратный ход.
If a(i) < a(i - 1) Then swap i, i - 1, bool
Next i
Конечно, за один прогон, массив будет отсортирован только в очень редких случаях, и данный метод подразумевает неопределенное (необходимое и достаточное) количество прогонов для достижения желаемого результата Но поговорим о прямом и обратном прогонах. В чем их отличие? И почему метод называется «методом пузырька»?
При прямом прогоне слева направо устремляются более крупные числа, как пузырьки воздуха всегда устремляются вверх.
Если на первом месте было максимальное число данного массива а(1)=max, то при прямом прогоне оно беспрепятственно
на каждом очередном шаге займет второе, третье и наконец последнее, самое правое место в массиве a(sizeArr)=max.
Если же это было не самое большое число (но и не самое маленькое), то оно тоже устремится направо, пока не встретит
на своем пути более крупное число. Дальше путь к вершине продолжит уже это новое более крупное число.
Вспомните, как большие пузырьки всегда всплывают быстрее
Таким образом, за один прямой прогон массив отсортирован не будет, но его последним элементом станет обязательно максимальное по величине число. При этом первым элементом массива станет наименьшее из чисел, располагавшихся на первом и втором местах.
А при единственном обратном прогоне (не забывайте, что массив сортируется по возрастанию)
первым элементом массива станет минимальное число. Про остальные ничего определенного сказать нельзя,
кроме того, что каждое более мелкое
число по сравнению со своим левым соседом, обменялось с ним местами.
За второй обратный прогон, вторым элементом станет второе по «мелкости» число. Оно никак не сможет занять первое место,
так как там уже находится минимальное в массиве число. Поэтому сделаем однозначный вывод, что каждый последующий
прогон целесообразно заканчивать на шаг раньше предыдущего. Этим сэкономим немного машинного времени.
Так сколько же раз нужно выполнить прогоны, чтобы массив полностью был отсортирован?
Конечно, для полной уверенности и 100% гарантии можно любой из прогонов (это без разницы) выполнить sizeArr-1 раз.
К гадалке не ходи, все элементы будут расположены по возрастанию. Но при этом вполне вероятно, что последние прогоны
проходили бы уже без замен элементов, так как последние элементы были расположены по порядку и условие на замену не выполнялось.
Вот, чтобы исключить, подобное и сэкономить еще немного машинного времени, используют «флаг сортировки», т.е.
обычную логическую переменную, которая до начала прогона имела бы значение true. Даже при единственной замене двух «соседей»
за весь прогон, в процедуре swap данный флаг сбросится. Но зато уж, если после прогона флаг остался равным true,
то можно с уверенностью прекращать сортировку, т.к. из всех пар соседних элементов, ни одна не выразила желание поменяться местами.
Это та же самая 100% гарантия, что и при избыточности прогонов.
Private Sub prForward(p As Integer, q As Integer, bool As Boolean)
Dim i As Integer
bool = True
For i = p To q 'прямой ход. максимальный элемент займет самое правое место
If a(i) > a(i + 1) Then swap i, i + 1, bool
Next i
End Sub
Private Sub prBack(p As Integer, q As Integer, bool As Boolean)
Dim i As Integer
bool = True
For i = p To q Step -1 'обратный ход. min-элемент займет самое левое место
If a(i) < a(i - 1) Then swap i, i - 1, bool
Next i
End Sub
Вот так я написал две процедуры для прямого и обратного прогонов. Они мне еще не раз пригодятся. А Вы можете, при желании, обойтись и любой одной. Дело вкуса и конкретной решаемой задачи
И как результат привожу два варианта главной процедуры метода пузырьковой сортировки:
Public Sub sortPusir() 'двухпроходный
Dim i As Integer, j As Integer, bSorted As Boolean
For j = LBound(a) To UBound(a) - 1
prForward LBound(a) + j, UBound(a) - j, bSorted
If bSorted Then Exit For 'значит сортировка окончена
prBack UBound(a) - 1 - j, LBound(a) + j, bSorted
If bSorted Then Exit For 'значит сортировка окончена
Next j
End Sub
bSorted флаг сортировки. Его даже инициализировать не надо, т.к. он однозначно устанавливается в
true перед каждым прогоном в процедурах прямого и обратного прогона.
Хочу отметить, что хотя цикл по j определен до UBound(a) 1, но реально он даже до середины
не дойдет, т.к. при двухпроходном цикле выход по флагу сортировки может осуществиться после любого из прогонов.
Public Sub sortPusir1() 'однопроходный
Dim i As Integer, j As Integer, bSorted As Boolean
For j = LBound(a) To UBound(a) - 1
prBack UBound(a), j + 1, bSorted
If bSorted Then Exit For 'значит сортировка окончена
Next j
End Sub
В однопроходном алгоритме все еще проще. Обратите внимание, что цикл по j идет на увеличение, а прогоны обратные, поэтому все прогоны будут начинаться от самого верхнего индекса массива, а заканчиваться на шаг раньше, чем предыдущий прогон.
скачать xls-файл для тестирования
Алгоритм Хоара или быстрая, рекурсивная сортировка
Понятное дело, раз алгоритм основан на рекурсии (т.е. при определенных условиях должен вызывать сам себя с измененными входными параметрами), то входные параметры этой процедуры заслуживают особого внимания.
Public Sub sortHoara(p As Integer, q As Integer)
Входные параметры p и q - это начальный и конечный индексы диапазона сортировки массива.
Т.е. вполне возможно провести сортировку не всего массива, а какой-то определенной его части.
Кстати, сам алгоритм так и поступает: после первой приблизительной сортировки всего диапазона массива,
вызываются сортировки его левой и правой части по отдельности. Каждая из этих частей, в свою очередь,
после собственной грубой сортировки, снова запустит сортировку своих левой и правой частей. И так до тех пор,
пока диапазон сортировки не сузится до пары элементов
А у пары элементов понятия грубой сортировки не существует. Обменяются они местами или не обменяются это и будет
самая точная сортировка самого маленького по размеру диапазона.
Каким же образом алгоритм проводит грубую сортировку? И как происходит деление на левую и правую части для последующей сортировки?
Первым делом процедура проверяет входные параметры на соответствие и принимает решение о продолжении или завершении своей работы, а вот вторым шагом (если решила продолжать выполняться) она определяет ОПОРНОЕ ЗНАЧЕНИЕ. Для хранения опорного значения в процедуре выделена отдельная переменная того же типа, что и хранящиеся элементы массива. В моем случае это r As Integer, но если в массиве будут храниться действительные числа или строки, то и опорное значение должно быть того же типа. Кроме того, опорное значение должно быть обязательно «больше или равно» минимальному элементу массива и «меньше или равно» максимальному.
ГРУБАЯ СОРТИРОВКА подразумевает перемещение любого элемента, который больше «опорного значения» в правую часть массива, и любого, который меньше «опорного значения», в левую часть (если сортировка по возрастанию, а иначе - наоборот). В идеальном варианте, «опорное значение» хотелось бы определить таким, чтобы ровно половина элементов массива его превышала, а половина массива была меньше него. Именно при таком варианте количество рекурсивных вызовов было бы минимальным, а, следовательно, и время выполнения сортировки.
А в самом тривиальном случае, r можно присвоить первое попавшееся значение массива, например: r=a(p) или r=a(q). Это будет вполне удовлетворять условиям выбора опорного значения, правда, про оптимальность времени выполнения алгоритма здесь вспоминать не будем. А если честно, то при таком выборе r и большом размере массива при определенных условиях алгоритм не сможет завершиться из-за переполнения стека (ведь каждый рекурсивный вызов это дополнительное наполнение стека).
Но не будем отвлекаться, и продолжаем рассматривать самый тривиальный случай с выбором r=a(p). В несортированном массиве, по теории вероятности, это будет какое-то промежуточное число между максимальным и минимальным элементами массива.
Третьим шагом, процедура ищет элемент (т.е. определяет индекс i элемента), который больше r, начиная с начала диапазона.
Четвертым шагом, процедура ищет элемент (т.е. определяет индекс j элемента), который меньше r, начиная с конца диапазона.
При выполнении условия If i < j And a(i) > a(j) Then swap i, j, False , как видим, происходит обмен (пятый шаг). Учитывая, что шаги 3-5 производятся в цикле Do While , то после окончания цикла, в левой части массива элементы будут располагаться беспорядочно, но среди них не будет ни одного большего r. Точно так же, в правой части, среди беспорядочно расположенных элементов, не будет ни одного меньше r. Это и есть грубая сортировка (по крайней мере, я для себя ее так называю). А значение j разделит массив на левую и правую части.
Следующими шагами процедуры (т.е. алгоритма) будут поочередная обработка левой и правой частей массива, путем рекурсивного вызова себя самой.
Вот пример такой, самой незамысловатой, процедуры сортировки по алгоритму Хоара:
Public Sub sortHoara_s(p As Integer, q As Integer)'самый простой вариант
Dim i As Integer, j As Integer, r As Integer
If p < q Then 'если на входе одинаковые или обратные индексы, то на выход
r = a(p) ' опорное значение
i = p - 1: j = q + 1 ' отступление за границы, чтобы не нарушать while
Do While i < j ' поиск элементов для обмена
Do
i = i + 1
Loop While a(i) < r
'i останавливается на элементе больше опорного (который надо направо)
Do
j = j - 1
Loop While a(j) > r
'j останавливается на элементе меньше опорного (который надо налево)
If i < j And a(i) > a(j) Then swap i, j, False ' обмен
Loop
sortHoara_s p, j ' сортируем левую часть
sortHoara_s j + 1, q ' сортируем правую часть
End If
End Sub
Если на вашем компьютере массив нужной размерности можно отсортировать несколько раз подряд (т.е. повторно
сортировать отсортированный массив), то можете дальне не читать. А на одном моем ноутбуке при повторной сортировке
выскакивает окно сообщения об ошибке переполнения стека.
Это понятно. Принимая за опорное значение самый левый
элемент отсортированного массива, программа делит массив на две части: в левой части 1 элемент, а в правой весь массив
без первого элемента. Вызывается рекурсивно левая часть и заканчивается мгновенно, а вот правая часть опять делится на 1 элемент
и все остальное. Итого для завершения задачи должно произойти sizeArr-1 рекурсивных вызовов. При достаточно большом
sizeArr и большом количестве элементов массива расположенных в порядке возрастания, такой момент должен наступить
неминуемо. Область памяти, отводимая под стек имеет свой предел...
Но если внести незначительные изменения
Public Sub sortHoara(p As Integer, q As Integer)
Dim i As Integer, j As Integer, r As Integer, bSorted As Boolean
If p < q Then 'если на входе одинаковые или обратные индексы, то на выход
If GetSortedMaxMin(p, q, mx, mn) Then Exit Sub
'если участок уже отсортирован - на выход
r = Round((mx + mn) / 2) ' опорное значение. Оптимально по середине
i = p - 1: j = q + 1 ' отступление за границы, чтобы не нарушать while
Do While i < j ' поиск элементов для обмена
Do
i = i + 1
Loop While a(i) < r
'i останавливается на элементе больше опорного (который надо направо)
Do
j = j - 1
Loop While a(j) > r
'j останавливается на элементе меньше опорного (который надо налево)
If i < j And a(i) > a(j) Then swap i, j, False ' обмен
Loop
sortHoara p, j ' сортируем левую часть
sortHoara j + 1, q ' сортируем правую часть
End If
End Sub
Где функция GetSortedMaxMin(p, q, mx, mn) возвращает «true» если заданный диапазон массива уже отсортирован,
что ведет к выходу из данного рекурсивного вызова. А если диапазон не отсортирован, то в параметрах по ссылке mx, mn будут
находиться максимальный и минимальный элементы массива соответственно, что позволит, более оптимально, определить
«опорное значение». Хотя и этот вариант, конечно, не на все случаи жизни Он просто немного лучше предыдущего…
Сортировка Слиянием и Хоара - совмещение
Совмещение алгоритмов Хоара и сортировки слиянием является наиболее оптимальным
Алгоритм сортировки слиянием отлично описан в Рунете.
Не сложно понять, что наибольший эффект от сортировки слиянием получается при объединении двух отсортированных массивов. А в начальный период, когда идет дробление исходного массива на части (как правило, до какой-то определенной величины, а то и до элемента), машинное время и память используются крайне не эффективно.
Как же тут не вспомнить про быструю, рекурсивную сортировку (Хоара). В том алгоритме все наоборот. Очень быстро сортируются сравнительно малые массивы (равномерно перемешанные), а в случае очень больших массивов (особенно если определенная часть уже отсортирована) может происходить рекурсивное переполнение стека.
Вывод: сортировку слиянием следует совмещать с быстрой сортировкой.
Не дробить начальный массив до элемента, а лишь до величины заданной константой MIN_CHUNK_SIZE и эти куски сортировать быстрой сортировкой, ну, а объединять потом, конечно, слиянием.
Таким образом, процедуру, объединяющую два предварительно отсортированных участка массива, можно представить так:
Public Sub merge(p As Integer, m As Integer, q As Integer)
Dim tmp() As Integer 'временный результирующий массив
Dim i As Integer, j As Integer, r As Integer счетчики
ReDim tmp(p To q)
i = p: j = m: r = p
Do
If a(i) < a(j) Then
tmp(r) = a(i)
i = i + 1: r = r + 1
Else
tmp(r) = a(j)
j = j + 1: r = r + 1
End If
Loop While i < m And j <= q 'пока не закончится один из массивов
Do While i < m 'пока не закончится второй из массивов
tmp(r) = a(i)
i = i + 1: r = r + 1
Loop
Do While j <= q 'пока не закончится второй из массивов
tmp(r) = a(j)
j = j + 1: r = r + 1
Loop
For i = p To q перезапись объединенного массива в исходный
a(i) = tmp(i)
Next i
End Sub
В виде параметров эта процедура получает три индекса элементов исходного массива:
- р - начальный индекс первого массива, он же будет и начальным индексам объединенного массива;
- m (средний) индекс являющийся начальным во втором массиве, поэтому первый отсортированный массив (или участок исходного массива) конечным индексом будет иметь m-1;
- q конечный индекс второго отсортированного и объединенного массивов.
А основная процедура сортировки, которая рекурсивно разбивает исходный массив на части длиною меньше константы MIN_CHUNK_SIZE и сортирует их, вызывая метод Хоара, а затем отсортированные части объединяет слиянием, может быть представлена так:
Public Sub mergesort(p As Integer, q As Integer)
Dim leng As Integer, midl As Integer, i As Integer
If p <= q Then 'если на входе одинаковые или обратные индексы, то ошибка - на выход
leng = q - p 'длина участка массива
If leng > MIN_CHUNK_SIZE Then
midl = leng / 2 'индекс элемента, разделяющего массив пополам
mergesort p, p + midl 1 'сортируем левую часть
mergesort p + midl, q ' сортируем правую часть
merge p, p + midl, q ' объединяем слиянием
Else
sortHoara_s p, q ' сортируем Хоаром
End If
End If
End Sub
В этом варианте никогда не происходит переполнения стека (ведь всегда можно уменьшить константу MIN_CHUNK_SIZE) и скорость сортировки достаточно хорошая
Тестируйте скачать xls-файл для тестирования
Другие примеры на тему «Алгоритмы Сортировки»
Другие примеры на языке «Visual Basic for application - VBA»
ЕЩЁ ПРИМЕРЫ:
C# Visual Studio 2010 .NET Framework 4
Сортировка слиянием массива записей (структур)
Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку ...
Поделиться в соц сетях:





