Как написать программу решения дифференциального уравнения… ( C++ )

Для C# здесь...

Для численного решения обыкновенных дифференциальных уравнений различают задачи с начальными условиями (ЗНУ) и граничными условиями (ЗГУ).

Дело в том, что для полного определения искомой функции одного уравнения недостаточно. При определении первообразной из производной функции мы получим множество решений, отличающихся друг от друга свободным членом (константой С).

Поэтому, для однозначного определения данной константы С, у искомой функции должны задаваться еще граничные условия, указывающие, что делается на концах исследуемого интервала, и/или начальные условия, описывающие значение функции
в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.

Для численного решения обыкновенных дифференциальных уравнений применяют метод Рунге-Кутта, с наиболее часто используемым 4-ым порядком точности. Давайте рассмотрим программную реализацию данного метода Рунге-Кутта, и Вы увидите, что написать программу для решения дифференциального уравнения не составляет особого труда.

Вариант решения задачи рассмотрю на следующем примере:

Условия задачи:
Пусть выстрел из орудия произведен с начальной скоростью V₀, под углом к горизонту α, с высоты Н₀ расположения орудия, т.к. в реальности огонь может вестись с холма или из капонира (т.е. ниже уровня земли).
Считаем, что снаряд имеет форму шара с радиусом r, изготовлен из материала, имеющего определенную плотность ρ.
Построить траекторию полета снаряда Y(x) ,
указать максимальную высоту полета H_k , дальность падения снаряда X_k и время полета t_k , построить график скорости V(t) на отрезке [0,t_k].

Таким образом, исходные данные, которые пользователь может задать на форме:
     Начальная скорость V₀, м/с2
     Начальная высота H₀, м
     Угол выстрела α, ° (град)
     Плотность материала ρ, кг/м3
     Радиус r, м

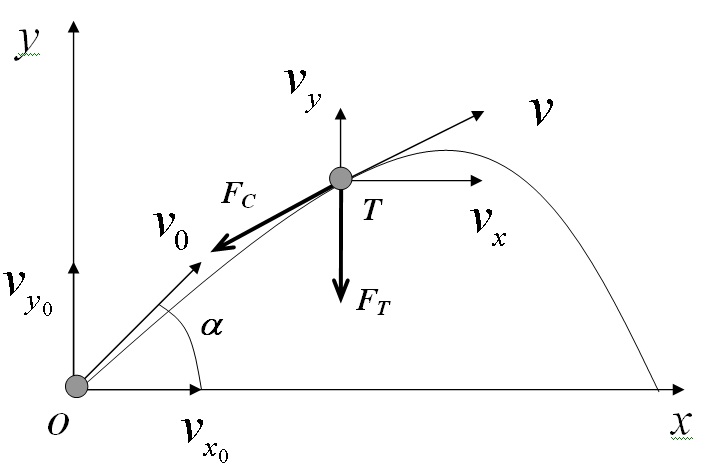
При построении математической модели условимся, что ось Оx системы координат направлена горизонтально в направлении выстрела, а ось Oy - вертикально вверх. Вектор скорости снаряда V(t) за время полета будет изменяться как по величине, так и по направлению, поэтому в модели рассматриваем его проекции на координатные оси. Горизонтальную составляющую скорости в момент времени t обозначим V_x(t), а вертикальную – V_y(t).

Пусть поверхность Земли плоская. Согласно законам механики, при сделанных предположениях движения тела в горизонтальном направлении является почти равномерным, а в вертикальном – равнозамедленным или равноускоренным с ускорением свободного падения g.

Если с силой тяжести F_T все достаточно просто (она свой вектор не меняет ни по величине, ни по направлению), то сила лобового сопротивления F_C , действующая на снаряд, пропорциональна квадрату скорости движения тела. Обозначим через F_X и F_Y горизонтальную и вертикальную проекции вектора силы лобового сопротивления,
причем      F_X/F= V_X/V,      F_Y/F= V_Y/V.

Значение силы лобового сопротивления F= -b·V² (пропорционально квадрату скорости тела). Коэффициент b=0.5·C·S·ρ, где C – коэффициент лобового сопротивления (для многих задач баллистики C≈0.15), S – площадь поперечного сечения (S=πr²), ρ - плотность воздуха (ρ=1,29 кг/м3).

Решение поставленной задачи можно свести к решению системы дифференциальных уравнений

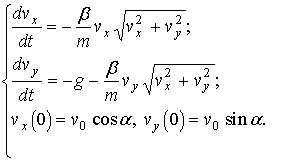
Метод Рунге-Кутта предполагает многократное вычисление значения производной искомой функции по имеющейся формуле (из уравнения), поэтому имеет смысл выделить их в отдельные подпрограммы…

Код функций будет выглядеть так:

// функция Нахождение горизонтальной проекции скорости
//по первому уравнению системы
double Form1::fvx( double vy, double vx )
{
     return -b*vx*sqrt(vx*vx+vy*vy) / m;
}

// функция Нахождение вертикальной проекции скорости
//по второму уравнению системы
double Form1::fvy( double vy, double vx )
{
     return -b*vy*sqrt(vx*vx+vy*vy) / m - g;
}


Шаг интегрирования у меня задается на форме.
Сейчас нам предстоит вычислить значения нескольких функций (V_x, V_y, V ) в точках заданного интервала с заданным шагом. В моем примере у интервала задано начало х=0, а конечная точка интервала будет определена в процессе вычисления (по условию: высота полета ядра стала <=0).
Результаты вычислений помещаются в массивы…

Код процедуры будет выглядеть так:

Void Form1::Runge_Kutta(void)
{
     double k1,k2,k3,k4, l1,l2,l3,l4;

     pY[0]=H; pX[0]=0; pt[0]=0; //массивы-координаты: высота, дальность и время
     pVx[0]=Vx; pVy[0]=Vy; pV[0]=V; //массивы- скорости: проекции на
             //горизонталь и вертикаль и полная скорость (величина вектора)
     bool vzbool=true;//взлет
     int i=1;

     //расчет по модели и заполнение массивов
     while( (pY[i-1]>-0.00001 || vzbool) && i<N )
     {
         pt[i] =pt[i-1]+_h;
         k1 = _h * fvx( pVy[i-1], pVx[i-1]);
         l1 = _h * fvy( pVy[i-1], pVx[i-1]);
         k2 = _h * fvx( pVy[i-1]+l1/2, pVx[i-1]+k1/2 );
         l2 = _h * fvy( pVy[i-1]+l1/2, pVx[i-1]+k1/2 );
         k3 = _h * fvx( pVy[i-1]+l2/2, pVx[i-1]+k2/2 );
         l3 = _h * fvy( pVy[i-1]+l2/2, pVx[i-1]+k2/2 );
         k4 = _h * fvx( pVy[i-1]+l3, pVx[i-1]+k3 );
         l4 = _h * fvy( pVy[i-1]+l3, pVx[i-1]+k3 );

         //вот собственно формула, определяющая метод Рунге-Кутта:
         // получаем проекции скорости из предварительно полученных
         //приближенных значений
         pVx[i]=pVx[i-1] + (k1+2*k2+2*k3+k4)/6;
         pVy[i]=pVy[i-1] + (l1+2*l2+2*l3+l4)/6;

         pV[i] = sqrt( pVx[i]*pVx[i] + pVy[i]*pVy[i] ); //величина вектора скорости
                 //из проекций

         pY[i]=pY[i-1]+pVy[i]*h;
         pX[i]=pX[i-1]+pVx[i]*h; //пересчет координат

         if(pY[i]>pY[i-1]) iMax=i; //сохранение номера узла с максимальной высотой
         else vzbool=false;//падение

         i++;
     }
     n=i-1; //количество реальных шагов
}


где:
         int iMax; //узел с макс.высотой полета

     double b; //коэф.пропорциональности Силы лобового сопротивления
     double m; //масса ядра
     double H; //уровень расположения орудия в момент выстрела
     double V,Vx,Vy; //начальная скорость и ее проекции на оси

В результате работы этой подпрограммы произойдет численное решение задачи Коши для системы обыкновенных дифференциальных уравнений и будут получены значения функций V_x(t_i), V_y(t_i) в точках t_i=i·h, i=1,2,...; h – шаг метода.

Как видим, после получения нового значения скорости V_x(t_i)
рассчитывается координата X(t_i)=X(t_i-1)+h·V_x(t_i), где h= t_i-t_i-1 = const.
Кроме того, параллельно рассчитывается значение высоты Y(t_i)=Y(t_i-1)+h·V_y(t_i),
где h= t_i-t_i-1 = const по найденным значениям V_y(t_i).
Когда будет получено значение Y(t_i)<0, вычисления заканчиваются
(немного модифицировано в условиях цикла while).

Кроме того, в программе интерполируются функции y(t), у(х) для нахождения более точных значений дальности и времени полета, а также максимальной высоты траектории. Полученные при интерполяции данные используем для построения траектории полета снаряда с более мелким шагом, например h=0,02 (сек).

Также в программе для сравнения проведен расчет по упрощенной модели, известной как модель Галилея, пренебрегая сопротивлением воздуха.

Вид формы:

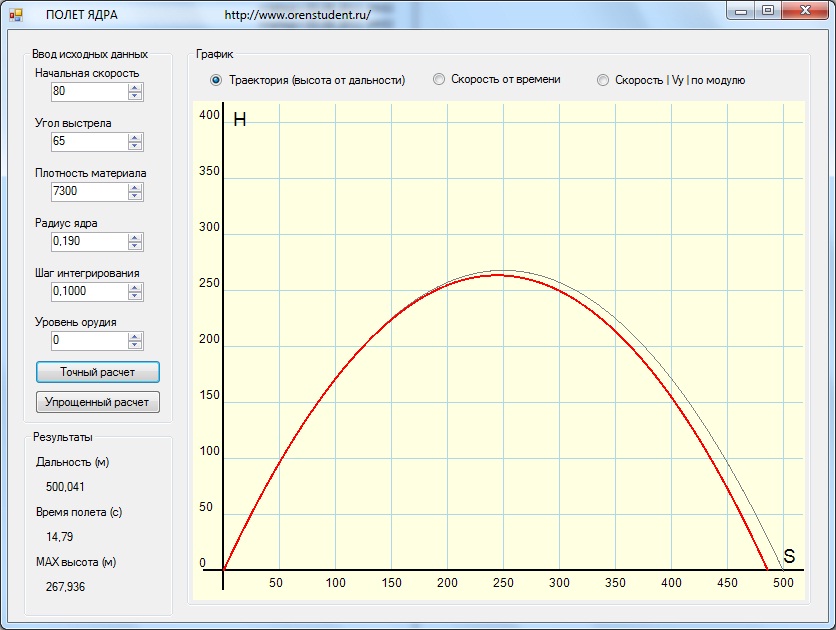
скачать exe-файл для тестирования

для Windows 10 скачать exe-файл для тестирования

Желающим, УДАЛЕННО (или В ФОРМЕ РЕПЕТИТОРСТВА), объясню материал
на примере ИХ ВАРИАНТА ЗАДАНИЯ…
Исходный код с подробными комментариями – на Ваш носитель или e-mail.

Удачи!

Другие примеры на тему «РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»

Другие примеры на языках «C»,«C++»,«C#»




Поделиться в соц сетях:

Если на этой странице не нашлось того, что Вы так искали...

         Не расстраивайтесь, не все потеряно... Смело щелкайте...