Программа тестирования
решения дифференциальных уравнений методом Рунге-Кутта.

Тестирование буду строить следующим образом:

1. выбираю функцию (в виде уравнения) у=v(x), т.е. такую функцию, которая должна получиться в результате решения… ;
2. Дифференцирую ее ( f(x)=v’(x) )…
3. И полученную функцию ( y’=f(x) ) подаю на вход программного алгоритма
4. Если на выходе программы в табличной и графической формах получится функция близкая к у=v(x), то алгоритм построен правильно (и можно оценивать погрешность, т.е. отклонение между истинными и вычисленными значениями)

Конечно, для качественного тестирования, желательно использовать не одну функцию, а несколько (определенный спектр) функций.

В программе добавление новых функций будет оформлено в виде двух отдельных подпрограмм.

function reshen(x:Extended):Extended; //функция-решение (эталонная)

, которая «помнит» заданный программистом спектр функций.

И соответственно, очень похожая по строению функция

function func(x:Extended;y:Extended=0):Extended; //производная

, которая «помнит» спектр соответствующих производных для функций.

Т.е. если мне в последующем надо будет проверить как интегрируется еще одна функция, то будет достаточно внести изменения в эти две функции (эталонное решение и его производную).

Поскольку, метод Рунге-Кутта решает задачу Коши, то на форме присутствует окно для ввода начальных условий у(а). Это позволяет вычислить константу в уравнении решения y=v(x)+C;

Суть работы программы: По исходным данным (интервал интегрирования и шаг) формируется массив x[i], и такой же размерности массив у[i], который заполняется по алгоритму Рунге-Кутта. Все крайне просто.

При работе с программой следует учитывать, что точность результата в значительной степени зависит от величины шага интегрирования (также задается на форме).

Вот пример, когда погрешность видна невооруженным взглядом….

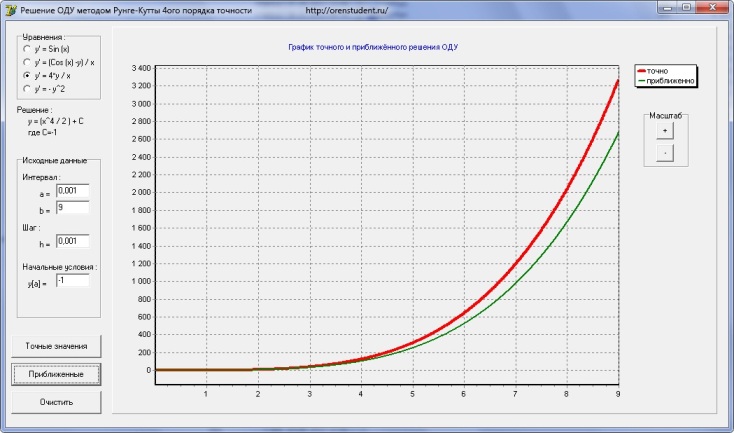
Но стоит только уменьшить шаг интегрирования в 10 раз и результат начинает радовать…

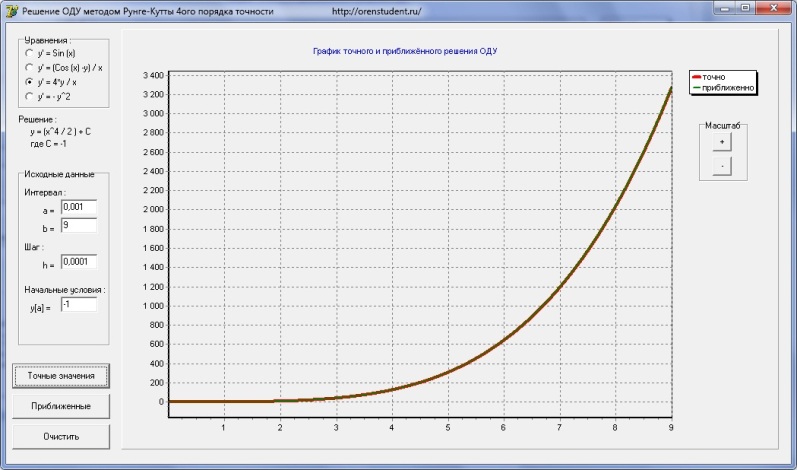
Еще необходимо помнить, что и функция и ее производная должны быть определены в каждой точке выбранного интервала интегрирования …

Иначе возможен такой вариант:

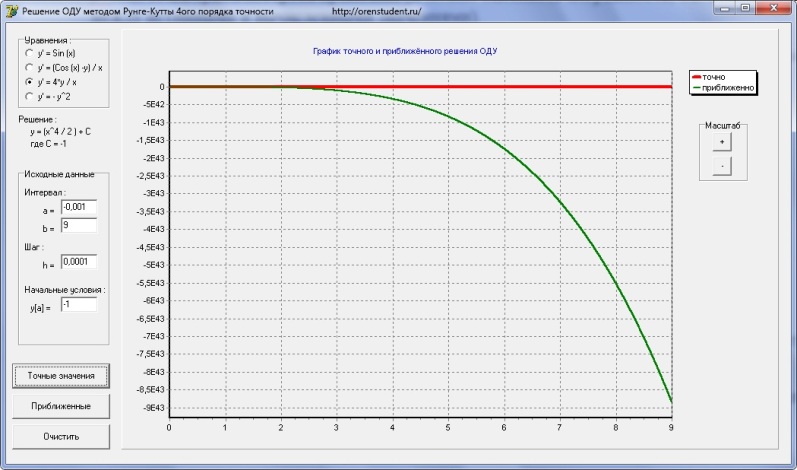
Винить некого!!!

Да, функция y=x^4/2 + C при С= -1 может иметь значение -1 в окрестностях точки х=0, но производная в этой точке y’=4y/x не определена. Поэтому тестируемый метод Рунге-Кутта в данном случае бессилен.

Меняйте интервал… (чтобы точка х=0 в него не входила).

Или можно изменить (программисту в коде) формулу производной y’=2x^3 (что одно и то же... см.формулы в предыдущем абзаце).

Но в этом случае точка х=0 в интервале интегрирования может присутствовать на общих основаниях…

Два видео об этой программе

Тестирование метода Рунге-Кутта

Если не удалось запустить видео, воспользуйтесь этой ссылкой ... видео на YouTube

Изменение тестируемых функций в коде программы

Если не удалось запустить видео, воспользуйтесь этой ссылкой ... видео на YouTube

Если качество (разрешение) Вас не устраивает, то Скачать видео на свой компьютер.

Удачного Вам тестирования! Ехе-файл скачать бесплатно.

Другие примеры на тему «РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»

Другие примеры на языке «Delphi»




Поделиться в соц сетях:

Если на этой странице не нашлось того, что Вы так искали...

         Не расстраивайтесь, не все потеряно... Смело щелкайте...