Отыскание экстремумов функции методом покоординатного спуска.
Код программы Delphi
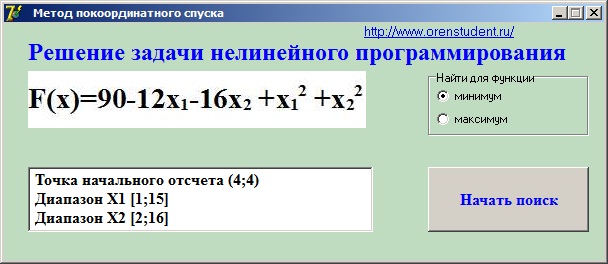
Рис.1 Учебная программа по алгоритму поиска экстремумов целевой функции методом покоординатного спуска
Семейство методов спуска служит для отыскания ТОЧКИ МИНИМУМА целевой функции…
Данный метод «Покоординатного спуска» является наиболее простым из этого семейства.
Следует заменить, что и ТОЧКУ МАКСИМУМА этим методом найти также просто (даже в названии замена слова «Спуск» на слово «Подъем» займет времени больше, чем корректировка условия…).
Исходные данные для метода спуска
Обязательными данными (условиями) для Метода Спуска являются:
- Размерность вектора (при n=2 – это точка на плоскости; при n=3 – точка в пространстве; и так далее до n-мерного пространства)
- целевая функция (т.е. ее коэффициенты при каждом из параметров, даже если это 0)
- точка начального отсчета (пусть случайная)
- точность (обеспечивается величиной шага h)
- желательно уточнить цель поиска (по умолчанию «Спуск» стремится к минимуму, поэтому при поиске максимума – акцентируем внимание особо)
- часто, по условиям задачи, накладываются ограничения на область определения, т.е. каждому из параметров выделяется определенный диапазон… Без этого, вполне возможно, задача не будет иметь решения, т.к. точка будет лежать где-то в бесконечности…
Ну и ответом, т.е. решением задачи – будет вектор (одномерный массив) параметров (что равносильно точке с координатами) на заданной области определения, обеспечивающий целевой экстремум . Как правило, к ответу пристёгивают и само значение целевой функции в найденной точке…
Алгоритм метода покоординатного спуска
Почему я называю этот метод наиболее простым в семействе?
Потому что он не требует использования производных функции… Пусть он не так быстр и оптимален, но в жизни простые алгоритмы не менее востребованы, чем быстрые, но сложные…
Допустим, ищем минимум…
Задаемся шагом h (обеспечивающим, заданную точность)
Начинаем менять первую координату, сохраняя все остальные как константы. Целесообразно, сначала шагнуть вправо и влево от начальной точки и определить знак перед h («+» или «-» , в какую сторону убывает целевая функция, туда и будем двигать текущую точку)… В цикле сдвигаем текущую точку на величину шага до тех пор, пока целевая функция не начнет расти или данная координата не выйдет за пределы заданного диапазона.
После этого начинаем менять следующую координату… Графически, этот процесс представляет собой перемещение текущей точки от положения начальной, на величину шага, вдоль соответствующих координатных осей (ортогональных направлений)…
При заданной ограничивающей области, текущая точка обязательно достигнет либо экстремума, либо границы области… (т.к. знак шага по данной координате определяется только один раз и не меняется до прерывания цикла)
Пояснения к исходному коду на DELPHI 7
function Z(aX:array of double):double; //целевая функция (менять здесь)
begin
Result:=90-12*aX[0]-16*aX[1]+aX[0]*aX[0]+aX[1]*aX[1];
end;
Целевая функция зависит от условия задания. Получает в виде параметра одномерный массив. Возвращает число с плавающей точкой двойной точности…
function Ztmp(idx:integer; dx:double):double;
var newPoint:array [0..n-1] of double;
i:integer;
begin
//целевая функция в точке смещения по заданной координате
for i:=0 to n-1 do
if i=idx
then newPoint[i]:=Cur[i]+dx
else newPoint[i]:=Cur[i];
Result:=Z(newPoint)
end;
Функция, получающая как параметры, номер координаты (т.е. ось направления) и величину смещения по этому направлению относительно текущей точки, и возвращающая значение целевой функции в этой новой точке newPoint …
function DefineZn(idx:integer; bMin:boolean=true):integer;
var tmp,tmp1,tmp2:double;
res:integer;
begin
//определение знака (по конкретной координате) 1 или 0 или -1, т.е. направления движения
tmp:= Z(Cur);
tmp1:= Ztmp(idx, -h);
tmp2:= Ztmp(idx, h);
if (tmp<tmp1) and (tmp<tmp2) or (tmp>tmp1) and (tmp>tmp2)
then res:=0 //экстремум
else if (tmp1<tmp2) Xor bMin //определяем знак по приращению и цели
then res:=1 else res:=-1;
if (Cur[idx]-h < R[2*idx]) and (res=-1) then res:=0; //смещение вниз не возможно
if (Cur[idx]+h > R[2*idx+1]) and (res=1) then res:=0; //смещение вверх не возможно
Result:=res;
end;
Функция определения знака, т.е. направления движения вдоль данной оси… Возвращает или 0, или 1, или -1, а параметрами служат номер координаты и тип разыскиваемого экстремума…
Кроме того, в расчетах используются координаты текущей точки – массив Cur[n] и массив ограничений по каждой из координат R[2*n] …
И вот, собственно, функция цикличного перемещения текущей точки от начала до экстремума
//поиск минимума методом координатного спуска
procedure TForm1.Koordinat_GoDown(bMin:boolean=true);
var i:integer;
boolEnd:boolean;//флаг окончания итераций
m,s,t:string;
begin
//поиск минимума методом координатного спуска
boolEnd:=false; // начальная инициализация для входа в цикл
SetNachal;
while Not boolEnd do
begin
boolEnd:=true;
for i:=0 to n-1 do //цикл по координатам
begin
zn:= DefineZn(i, bMin); //вход
while zn<>0 do
begin
boolEnd:=false; //сброс флага окончания
Cur[i]:=Cur[i] + h*zn; //смещение точки по конкретной координате
zn:= DefineZn(i, bMin); //переопределение знака
end;
end;
end;
//вывод результата
s:=FloatToStr(Z(Cur));
t:=FloatToStr(Cur[0])+'; '+FloatToStr(Cur[1]);
if bMin then m:= 'Минимальное' else m:= 'Максимальное';
ShowMessage(m+' значение целевой функции Z('+t+')='+s);
end;
Где
boolEnd - флаг окончания итераций (локальная переменная)
Истинность условия достижения экстремума или границы области if zn1=0
инициирует переход к следующей итерации then continue
else begin… , а иначе - циклическое смещение текущей точки («Спуск» по поверхности целевой функции)
Данный метод широко используется в задачах оптимизации, а также анализа функций с большим количеством параметров… Понятно, что этот метод способен найти только ближайшую точку эксремума... (т.е. любой локальный экстремум блокирует путь к абсолютному экстремуму)
Скачать ехе-файл для тестирования…
Другие примеры на языке «Delphi»
Поделиться в соц сетях:





