Математическая модель полета тела, брошенного под углом к горизонту

«Свободное падение» всевозможных тел мы имеем удовольствие наблюдать в повседневной жизни практически ежедневно.
Когда то это нас радует (примеры: плоды с дерева оказались на земле, за подстреленной уткой достаточно сделать несколько шагов, а не взлетать соколом). Огорчений тоже достаточно (град бьет все - от урожая до автомобилей; яблоко, а еще хуже кокос, а еще хуже кирпич на голову серьезное огорчение, а про метеориты даже вспоминать не хочется).

1. Параметры, влияющие на траекторию полета под углом к горизонту
2. Точность результата вычислений и сложность модели
3. Модель полета тела под углом к горизонту
4. Интерфейс приложения - возможности по изменению параметров задачи
5. Калькулятор траектории полета

Еще с древности люди стремятся использовать эти силы (лук и стрелы, катапульта и камень, пушка и ядро все метают снаряды под углом к горизонту). И заметьте, меткие стрелки всегда были в большом уважении (как Робин Гуд).
Поэтому появление такой науки, как баллистика абсолютно закономерно.

Параметры, влияющие на траекторию полета под углом к горизонту

Исходные данные, которые необходимо учитывать, при расчете траектории тела, брошенного под углом к горизонту:

     Начальная скорость V₀, м/с
     Начальная высота H₀, м
     Угол выстрела α, ° (град)
     Масса тела m, гр
     Диаметр D, мм
     Ускорение свободного падения g, м/c²
     Плотность воздуха (среды) ρ, кг/м³
     Коэффициент лобового сопротивления С.

Точность результата вычислений и сложность модели

Сложность математической модели вопрос не праздный. Все зависит от необходимой точности результата. Можно вообще сопротивлением воздуха пренебречь (если бросаешь кирпич рукой)…, но на дальние расстояния (особенно легкие предметы значительного объема) - ошибиться можно в разы.

Если копнуть глубже (это все про сложность модели): использование школьных констант g=9,8 (ускорение свободного падения) и ρ=1,29 (плотность воздуха) тоже не катит, так как в условиях морского побережья они будут больше, чем в условиях высокогорья. А если еще учитывать широту g будет расти по мере удаления от экватора и приближения к полюсам.

Радует только то, что для конкретных условий их (константы) можно подобрать опытным путем и дальнейшие вычисления запускать уже на этих значениях констант.

Модель полета тела под углом к горизонту

При построении математической модели условимся, что ось Оx системы координат направлена горизонтально в направлении выстрела, а ось Oy - вертикально вверх. Вектор скорости снаряда V(t) за время полета будет изменяться как по величине, так и по направлению, поэтому в модели рассматриваем его проекции на координатные оси. Горизонтальную составляющую скорости в момент времени t обозначим V_x(t), а вертикальную V_y(t).

Пусть поверхность Земли плоская. Согласно законам механики, при сделанных предположениях движения тела в горизонтальном направлении является почти равномерным, а в вертикальном равнозамедленным или равноускоренным с ускорением свободного падения g.

Интерфейс приложения - возможности по изменению параметров задачи

Это приложение является продолжением предыдущих учебных программ по моделированию свободного падения тел с учетом сопротивления воздуха. И, конечно, для сравнения строится траектория полета тела с этими же исходными параметрами, но без учета сопротивления атмосферы, т.е. по формулам модели Галилея.

Как и положено, по сравнению с предыдущими версиями, на лицо более широкие возможности по проведению опытов

• Графическое изображение системы координат позволяет пользователю настраивать ширину делений сетки (от 20 до 200 пикселей) и масштабировать линейные размеры системы (от 1 до 500 метров в деление сетки).
• Средние параметры таких констант, как плотность, вязкость, коэффициент лобового сопротивления воздуха установлены по умолчанию при старте программы, но экспериментатор может их изменить (допустим, если его интересует протекание процесса в высокогорных условиях). И даже, скажу больше: диапазон пределов настолько велик, что можно моделировать внеземные условия. Допустим, поднять плотность до значения, которое может существовать при давлении в 9 атмосфер Влияние вязкости воздуха (а вязкость газов возрастает с повышением температуры) учитывается по уравнению Стокса в виде силы торможения пропорциональной скорости снаряда (тела). И пусть ее влияние очень незначительно, но кому-то пригодится.
• При определении исходных данных, таких как начальная скорость и угол, масса и диаметр, а также уровень, с которого производится бросок или выстрел допускается ввод дробных чисел, обеспечивая тем самым любую необходимую точность. Параметр «Уровень» H₀ , то есть высота расположения тела перед броском, может иметь как положительные, так и отрицательные значения (т.е. выше или ниже уровня земли).

Программа строит траекторию полета тела Y(x) брошенного под углом к горизонту, и кроме того, используя параболическую интерполяцию, с высокой точностью определяет дальность полета Xk, максимальную высоту полета Hk , время полета tk , а так же время (взлета) достижения телом максимальной высоты, и координату Х (взлета), при которой максимальная высота достигнута.

Видеоинструкция:

Если не удалось запустить видео, воспользуйтесь этой ссылкой ... видео на YouTube

Решение поставленной задачи сведено к решению системы дифференциальных уравнений, т.е. численному решения задачи Коши для системы обыкновенных дифференциальных уравнений. Для решения задачи Коши здесь используется простой в реализации метод Рунге-Кутта 4-порядка, обеспечивающий достаточно высокую точность вычислений. Шаг интегрирования составляет 0,01 секунды Но кроме того, точное положение интересующих «контрольных» точек (а именно: падения и максимальной высоты), которые чаще всего располагаются между узлов сетки, вычисляются решением квадратных уравнений интерполируются

Уменьшая (до минимума) значения плотности и вязкости воздуха, можно видеть как кривые графиков (вакуума и атмосферы) сливаются в одно целое. Это подтверждает правильность построения математической модели, а несколько реальных опытов поможет Вам подобрать коэффициенты (константы) для конкретно Ваших атмосферных условий.

Калькулятор траектории полета

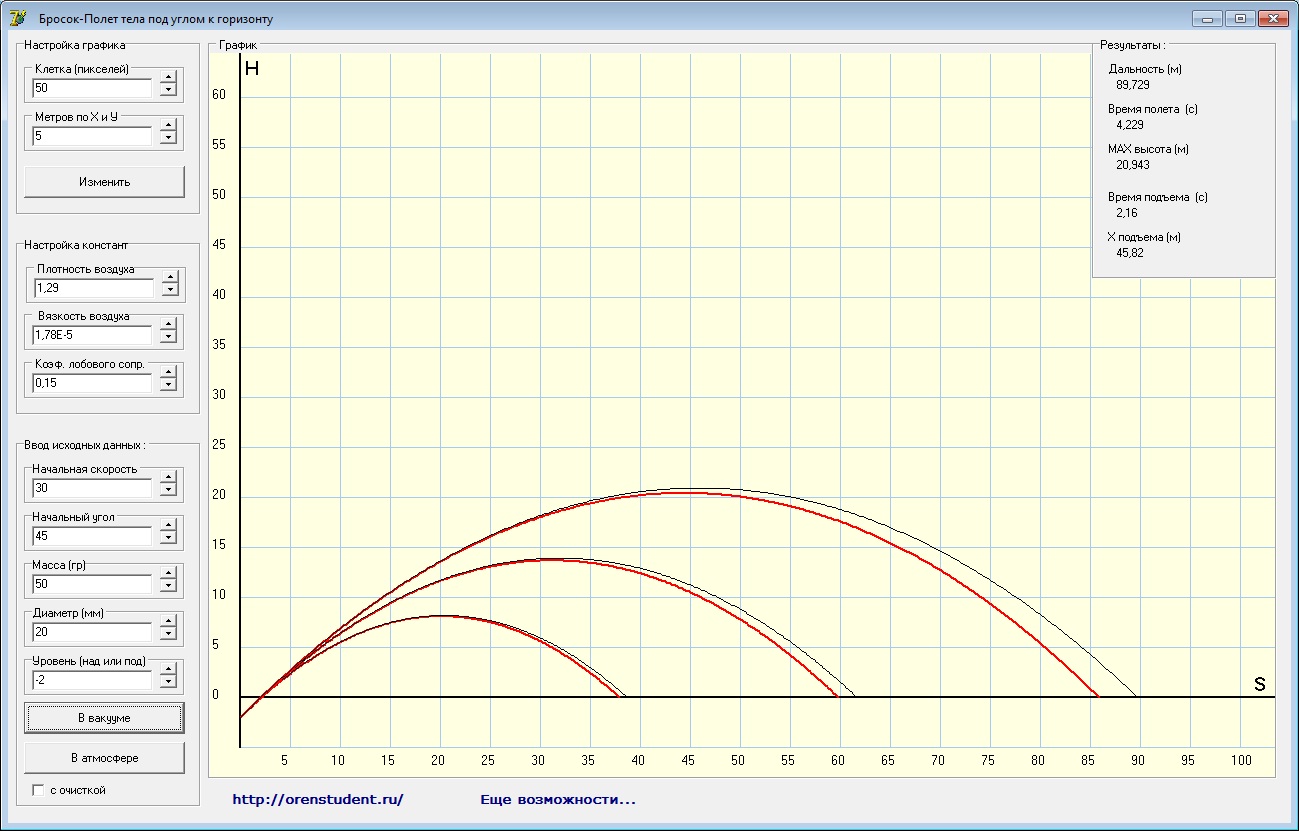
Рис.1        Калькулятор траектории полета

На рисунке показаны траектории, для случаев, когда брошено одно и тоже тело под углом 45 градусов, но с разными начальными скоростями (20, 25, 30 м/с). Окно «Результаты» показывает значения последнего процесса (либо в вакууме, либо в атмосфере).

скачать ехе-файл для тестирования

Другие примеры на тему «РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»

Другие примеры на языке «Delphi»