Метод последовательных приближений (простых итераций) на Delphi
Предлагается программа, тестирующая метод последовательных приближений (простых итераций).
Актуально! Решение краевой задачи сеточными методами (высокого порядка точности) дает возможность автоматизировать такие сложные процессы, как решение систем уравнений с помощью построения разностных схем .
Постановка задачи:
Дифференциальная задача:
y''(x)=f(x,y(x));
f – заданная функция
K – число отрезков разбиения (узлов сетки), задается с клавиатуры.
[a,b] – рассматриваемый промежуток, задается с клавиатуры.
y(0) = φ, y(K)=ψ - краевые условия;
Используя заданную схему сеточной аппроксимации, решить систему сеточных уравнений методом последовательных приближений (простых итераций).
Заданная схема сеточной аппроксимации:
Для внутренних точек

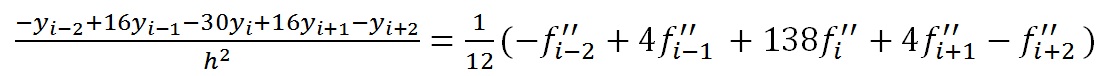
Для первого уравнения (i=1) предлагается
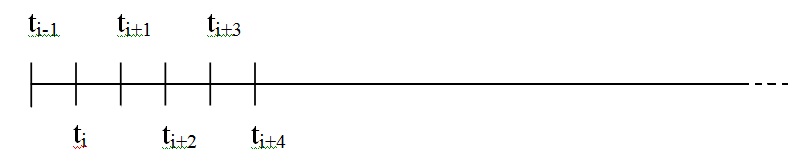
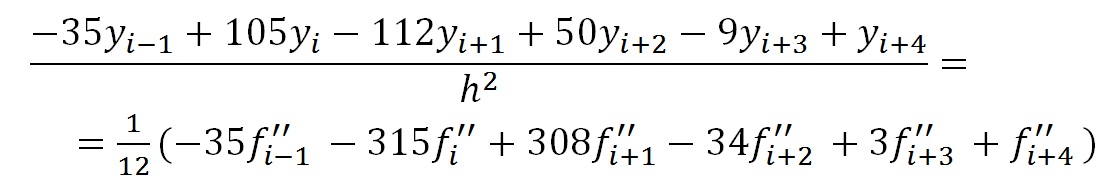
Для последнего уравнения (i=k-1) предлагается

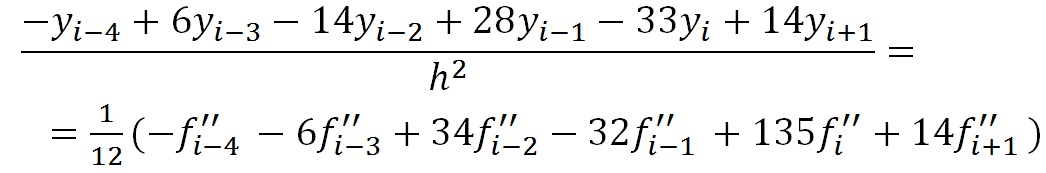
Решение:
Тестирование метода последовательных приближений (простых итераций) я решил продемонстрировать на примере 3 функций (разумеется, сначала брал решение, потом его дифференцировал и получал F(x,y,y’))
F(x) = 2y / x2 + 4yCos(x) / xSin(x) – y2 / x2Sin(x); //решением будет y= x2Sin(x) +C
F(x)= 2y' + 6x*ln(x)*(1-x) – 2x2 + 5x; //решением будет y= x3ln(x)+C
F(x):= y' 2 + 4y2 – 8y + 2;
//решением будет y= Cos2(x)+C
Поскольку я знаю формулы решения, то могу строить теоретически правильные графики для сравнения.
Задача, конечно, не тривиальна. Используются одновременно три разностных схемы.
Коэффициенты для каждой из них будут свои, и рассчитывать их надо аккуратно…
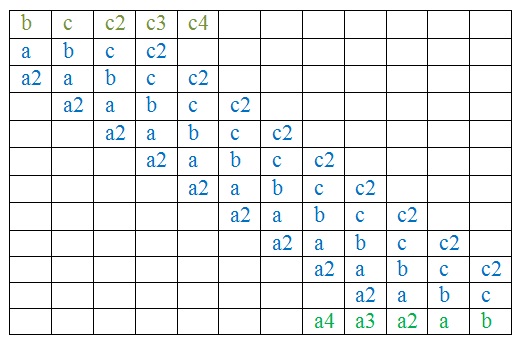
Получилась такая разряженная матрица (в пустых клетках, конечно, нули).
Чтобы изменить эталонные функции на другие, достаточно внести изменения в 3 функции программы:
//функция-решение (эталонная, теоретическая)
function reshen(x:Extended):Extended;
begin
reshen:=0;
Case numFunction of
0: reshen:=x*x*Sin(x);
1: reshen:=x*x*x*ln(x);
2: reshen:=Cos(x)*Cos(x);
3: reshen:=x*kk;
end;
end;
//функция-первая производная решения (эталонная, теоретическая)
function pr_reshen(x:Extended):Extended;
begin
pr_reshen:=0;
Case numFunction of
0: pr_reshen:=2*x*Sin(x)+x*x*Cos(x);
1: pr_reshen:=3*x*x*ln(x)+x*x;
2: pr_reshen:=-2*Sin(x)*Cos(x);
3: pr_reshen:=kk;
end;
end;
// fx - эти данные должны быть заданы как исходные (возможно, таблично), но для проверки алгоритма, программа использует эталонные функции
//заданная функция-вторая производная решения (по эталонным)
function fx(x,y:Extended):Extended;
begin
fx:=0;
Case numFunction of
0: if x<>0 then fx:=2*y/x/x+4*y*Cos(x)/x/Sin(x)-y*y/x/x/Sin(x); //нелинейность
1: if x<>0 then fx:=2*pr_reshen(x)+6*x*ln(x)*(1-x)-2*x*x+5*x; //линейность c производной
2: fx:=(pr_reshen(x))*(pr_reshen(x))+4*y*y-8*y+2; //нелинейность c производной
3: fx:=0;
end;
end;
А если необходимо найти решение реально (без сравнения с эталонами), то нужно заполнить массив F для каждого x[i] узла сетки и пусть последняя функция возвращает значения из этого массива для запрашиваемого узла. Две первые функции в этом случае не используются.
Метод итераций подразумевает:
получение значения функции в определенном узле сетки на основе значений этой функции в соседних узлах.
С каждой итерацией (последовательным приближением) значение функции (в каждом из узлов) становится все ближе к эталонному,
а величина, на которую изменилось значение (по сравнению с прошлой итерацией) – все меньше.
Поэтому перед началом решения следует задаться ε - допустимой ошибкой в решении и остановить цикл итераций,
как только изменение функции в каждом узле сетки станет меньше ε - допустимой ошибки.
Полученный массив остается вывести на график и в текстовое окно результата.
Ну, и сравнить с эталонной функцией…

Вот как классно совпадает график рассчитанный с теоретическим (точным)… Красная линия точно накладывается на зеленую... А черная тонкая - это fx - заданная функция-вторая производная.
Приобретайте код и тестируйте на своих функциях…
Или я могу ваши функции поместить в код…
Другие примеры на тему «РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»
Другие примеры на языке «Delphi»
Поделиться в соц сетях:





