Программа приведения разряженной матрицы (по Гауссу) к нужному виду

По определению, разряженные матрицы это те, что имеют значительную долю (процент) нулевых элементов. На рисунках ячейки с нулевыми элементами оставлены чистыми.

По ряду причин особый интерес вызывают диагональные разряженные матрицы.
Например, 3-диагональные и 5-диагональные разряженные матрицы очень удобно использовать для решения систем уравнений по разностным схемам.

Там также необходимо будет выполнить преобразование по Гауссу, но с целью приведения матрицы к виду «единичной».

Ну, а в этом задании, требовалось преобразовать разряженную матрицу определенного типа к виду «матрицы перемен».

Вид начальной матрицы (n x n):

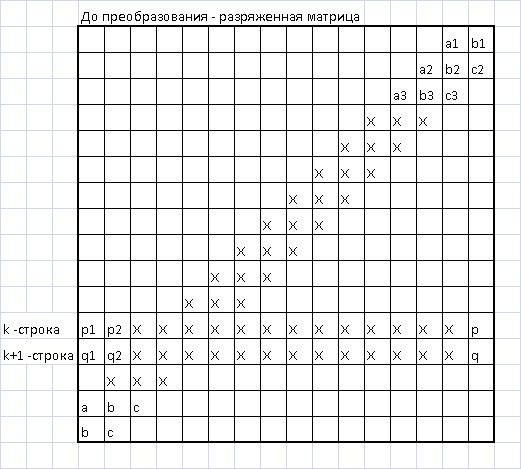
Как видим, заполнены три побочные диагонали и две строки. Остальные элементы равны 0.
Хранить разряженные матрицы (для экономии компьютерной памяти, учитывая, что в реальности размеры их могут быть очень большими) принято не в виде двумерного массива, а в виде отдельных векторов (одномерных массивов).
Так, для нашего случая, достаточно зарезервировать память под 5 векторов размерностью n: a,b,c,p,q.

На рисунке обозначены элементы векторов. Строки матрицы нумеруются, начиная сверху, а столбцы – начиная слева. Поэтому некоторые элементы разных векторов должны быть (именно для этой схемы матрицы) равны между собой ВСЕГДА.

То есть во время преобразований необходимо следить, чтобы если изменился элемент a_k+1 , то обязательно надо изменить и элемент q_n-k-1 .
А элемент c_k должен быть всегда равен p_n-k+2.
И так далее…

По условию задачи нужно привести данную матрицу к виду «матрицы перемен», не изменяя вектор Х, и проанализировать, как при этом изменяется вектор F.

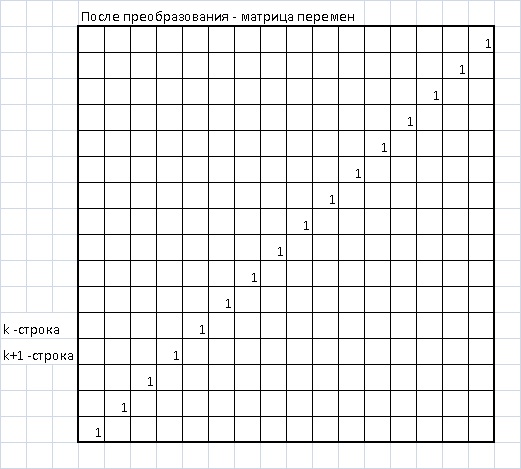
где вектор Х – это заданный (случайный) вектор, а вектор F - результат перемножения матрицы А на вектор Х. То есть уравнение в матричном виде будет выглядеть: А*Х = F.

Результат работы программы можете протестировать, скачав ехе-файл…
А выводы, об изменении вектора F сделаете сами…

После такого эксперимента нетрудно сделать вывод и об изменении вектора F в том случае, если преобразования матрицы будут проведены к виду «единичной матрицы», т.е. единицы в ней будут располагаться не по побочной, а по главной диагонали…

Если у кого-то возникнут задачи на похожие темы – всегда готов поучаствовать…

Другие примеры на тему «Матрицы и операции вычислений с ними»

Другие примеры на языке «Delphi»

Удачи!


Поделиться в соц сетях:

Если на этой странице не нашлось того, что Вы так искали...

         Не расстраивайтесь, не все потеряно... Смело щелкайте...