Программа, тестирующая метод трехточечной прогонки для «Решения краевой задачи дифференциального уравнения 2-го порядка» с помощью разностной схемы
Постановка задачи:
Дифференциальная задача:
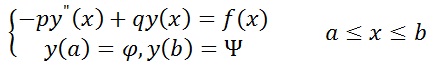
p,q – задаются с клавиатуры коэффициенты
f(x) – заданная функция
Выбрать схему сеточной аппроксимации и решить систему сеточных уравнений методом трехточечной прогонки.
Решение:
Основой численных методов решения краевых задач - является замена исходной системы уравнений ее сеточной аппроксимацией. В случае интегро-дифференциальных уравнений такая аппроксимация обычно строится с помощью разностных схем.
Не вдаваясь особо в теорию,
формулы для первой и второй производных в разностных схемах выглядят так:
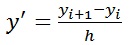
- характеризует скорость изменения функции
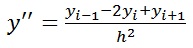
- характеризует кривизну графика функции
Разностных схем можно построить множество (дело вкуса) и все они будут давать приближенный результат решения дифференциального уравнения. А степень приближения, т.е. качество решения - зависит как раз от выбранной схемы и характера функции. Кому-то поможет опыт, кому-то везение…
Вот, я останавливаюсь на следующей схеме сеточной аппроксимации для заданного уравнения
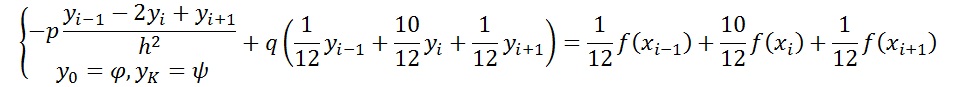
где i=1,2,…,K-1 (т.к. в узлах i=0 и i=K результат функции известен – краевые условия заданы!)
K- будет задаваться на форме (количество узлов сетки, будет определять шаг интегрирования)
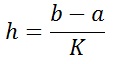
Тестирование метода трехточечной прогонки я решил продемонстрировать на примере 3 функций (разумеется, сначала брал решение, потом его дифференцировал и получал F(x))
F(x) = - p*(6*x^2)+q*(x^4)/2+C); //решением будет y(x)= (x^4)/2 +C
F(x)= - p*(-1/x^2)+q*(ln(x)+C); //решением будет y(x)= ln(x)+C
F(x):= - p*(-Cos(x))+q*(Cos(x)+C); //решением будет y(x)= Cos(x)+C
Поскольку я знаю формулы решения, то могу строить теоретически правильные графики для сравнения.
Расcчитав коэффициенты
a:= (q/12-p/h/h);
b:= (10*q/12+2*p/h/h);
c:=a; // (q/12-p/h/h);
для каждых последовательных трех узлов сетки можно записать
a*Yi+1 + b*Yi +c*Yi-1= F(xi+1,xi,xi-1)
Отличаться будут только первое и последние уравнения (т.к. там краевые условия заданы)
Первое : b*Yi +c*Yi-1= F(xi+1,xi,xi-1) - a*Y0
Последнее: a*Yi+1 + b*Yi = F(xi+1,xi,xi-1) - c*Yk
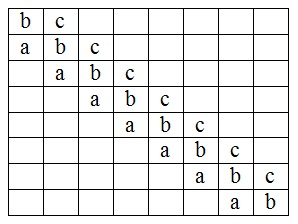
Получилась такая разряженная матрица (в пустых клетках, конечно, нули).
Сначала в массив y[i] помещаем значения F(xi+1,xi,xi-1) как вектор свободных членов…
Далее, методом трехточечной прогонки (преобразованиями Гаусса) приводим эту матрицу к единичной, и в результате в векторе-столбце F(x) , а значит и в массиве y[i] получаем искомые у(х[i]) для каждого узла сетки.
Полученный массив остается вывести на график и в текстовое окно результата.
Ну, и сравнить с эталонной функцией…
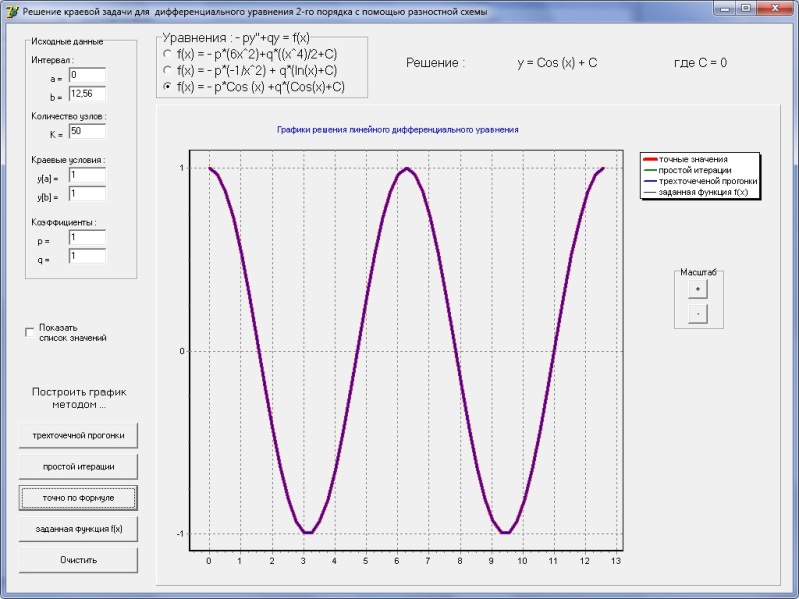
Вот как классно совпадает график рассчитанный с теоретическим (точным)…
Приобретайте код и тестируйте на своих функциях…
Или я могу ваши функции поместить в код…
Другие примеры на тему «РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»
Другие примеры на языке «Delphi»
Поделиться в соц сетях:





