Матричный калькулятор. Исходный код на Delphi. Решение СЛАУ (видео)

Данная программа является простейшим калькулятором для решения примеров с использованием матричной арифметики.
Простейший код для первокурсников. Берите и дорабатывайте...

1. Используемые в приложении компоненты Delphi
2. Сложение и вычитание матриц
3. Транспонирование
4. Определитель и обратная матрица
5. Умножение и деление матриц
6. Решение СЛАУ с помощью калькулятора
7. Исходный код на Delphi

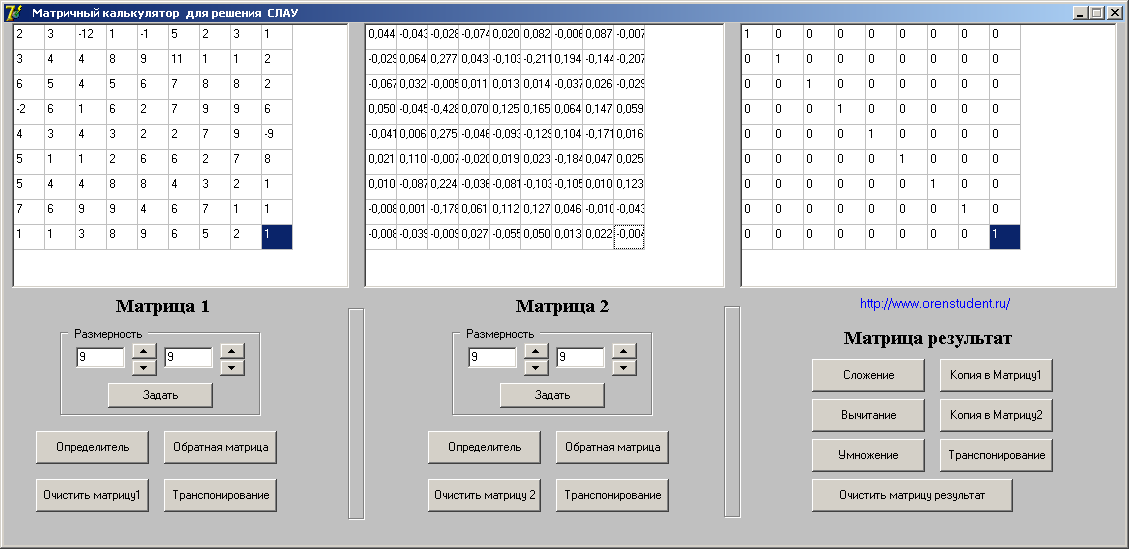
Рис.1        Результат перемножения матрицы на обратную (единичная матрица)

Используемые в приложении компоненты Delphi

• TStringGrid - таблица строк, позволяют отображать матрицы в виде таблиц (т.е. двумерных массивов) разных размеров (2х2, 3х3, 4х4, 5х5, 6х6, 7х7 и не только квадратные...) и вектора в виде строк и столбцов;
• TUpDown - кнопка-счетчик дает возможность избежать ошибок при вводе цифровой информации
• TEdit - окно для отражения важной информации, изменяемой элементом TUpDown
• TButton - командная кнопка, запускает целевое действие
• TGroupBox - для группировки элементов на форме (интуитивная связь)
• TLabel - лейбл, ярлык, пояснения...

Сложение и вычитание матриц

Обязательным условием для сложения и вычитания матриц является полное совпадение их размеров. И результирующая матрица будет иметь то же самое количество строк и столбцов, какое имели матрицы-слагаемые. Каждый элемент новой матрицы (с индексами i j) будет равен сумме элементов слагаемых матриц (с теми же индексами i j).

Как обычно, вычитание отличается от сложения только знаком. Чтобы поменять все знаки в матрице, достаточно умножить ее на «минус-единичную-матирцу» (т.е. такую матрицу, в которой главная диагональ полностью состоит из -1, а остальные элементы равны 0). Экспериментируйте...

Транспонирование

Операция перемещения элементов матрицы так, чтобы строки стали столбцами, и наоборот, столбцы - строками... Если матрица большого размера, то вручную такую операцию выполнять утомительно... и чревато ошибками...

Определитель и обратная матрица

Определитель (или детерминант) матрицы - это число, полученное в результате определенных операций над матрицей.

Обратная матрица (которая и обозначается как матрица в -1 степени) - матрица, полученная из первоначально заданной матрицы по определенным правилам. Произведение обратной матрицы на первоначальную дает единичную матрицу. Так А * А^-1 = Е .

Умножение и деление матриц

Обязательным условием для умножения матриц является совпадение количества столбцов первой матрицы и количество строк второй матрицы А результирующая матрица будет иметь то же самое количество строк, что и первая матрица, и то же самое количество столбцов, что и вторая матрица

Так если имеем матрицу А с размерами i,k и матрицу B с размерами k,j то результатом будет матрица С с размерами i,j. Каждый элемент новой матрицы (с индексами ij) будет равен сумме произведений элементов
i-строки первой матрицы на элементы j-столбца второй матрицы.

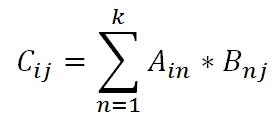
Или можно сказать, что каждый элемент новой матрицы будет равен скалярному произведению i-вектора-строки первой матрицы на j-вектор-столбец второй матрицы

А количество элементов в этих векторах должно обязательно совпадать

Деление матриц А на В заменяется операцией умножения А на обратную матрицу В^-1.
Тем самым, матрица В как бы попадает в знаменатель дроби, тогда как А остается в числителе.

Решение СЛАУ с помощью калькулятора

Пример решения системы линейных алгебраических уравнений (слау) приведен в видео...

Скачать видео... (без рекламы)

Если не удалось запустить видео, воспользуйтесь этой ссылкой ... видео на RuTube

Решение систем уравнений с помощью матриц является универсальным методом, а при использовании компьютера и самым быстрым. Размеры системы уравнений в этом случае не так критичны, как при ручном решении.
Алгоритм следующий:

1. Заполнить матрицу А коэффициентами при переменных из системы уравнений;
2. Найти обратную матрицу А^-1;
3. Умножить обратную матрицу на вектор-столбец свободных членов B;
4. Полученный вектор-столбец X и будет содержать значения переменных;

Исходный код на Delphi

Поскольку исходный код предлагаю очень дешево, то приводить листинг не буду...

Краткие пояснения:

1. Объекты класса TStringGrid (строковая таблица) не имеют метода очистки всех своих ячеек, поэтому очистка проводится через методы строк или столбцов См. процедуры-обработчики событий кнопок очистки, которые вызывают одну и ту же процедуру SG_clear, посылая в нее в виде параметра соответствующую StringGrid.
2. Процедура заполнения нулями procedure Full_0(sg:TStringGrid); необходима чтобы исключить ошибки конвертации пустых ячеек в числа
   Т.е. перед вычислениями производится проверка содержимого всех ячеек и если ячейка, по недосмотру пользователя, осталось пустой, то в нее помещается 0. Логично?

Тестирование - это наиболее важный этап в жизненном цикле программного продукта. Поэтому не верьте картинкам, фильмам и сказкам…

Только личное тестирование во всех наиболее сложных сочетаниях данных - должно убедить Вас в доброкачественности алгоритма и исходного кода!

скачать ехе-файл для тестирования

Другие примеры на языке «Delphi»

Другие примеры на тему «Матрицы и операции вычислений с ними»

Если на этой странице не нашлось того, что Вы так искали...