Алгоритм шифрования RSA. Длина ключа 512 бит
Учебная программа на C++ Visual Studio.
Задание:
Программно реализовать алгоритм шифрования и дешифрования с помощью открытого ключа - алгоритм RSA для любых типов файлов.
Реализовать создание цифровой подписи с использованием RSA для любых типов файлов, а также проверку на соответствие файла его цифровой подписи.
Решение:
На мой взгляд, первая часть задачи «Генерация ключей» RSA наиболее сложная.
Вторая часть наиболее легкая – это кодирование и декодирование.
Третья часть «Цифровая подпись» занимает промежуточное положение по сложности…
Но для того, чтобы приступить к любой из частей задачи, у Вас должен быть готов программный аппарат для «длинной арифметики».
Без этого никуда… При чем целесообразно максимальную длину (32 или 64, или 128 байт) задать константой,
чтобы можно было легко перестроить программу на другую длину пакета…
И так, первая часть:
Генерация открытого и закрытого ключей в алгоритме RSA
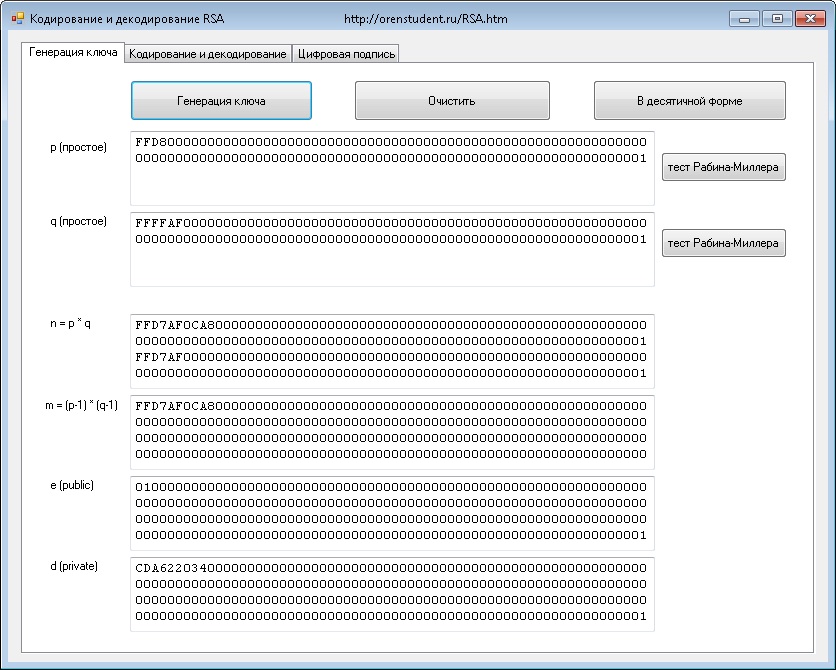
Цель: найти три длинных числа – n, e, d (модуль, открытая и закрытая экспоненты)! Их длины должны быть равны заданной длине пакета.
Прежде всего, находятся длинные простые числа p и q (их длина равна половине длины пакета).
Даже самый легкий и быстрый тест на простоту – «Тест Рабина-Миллера» (одноименные кнопки предназначены для каждого из чисел) заставляет поскучать у компьютера в ожидании результата…
Для скорости последующих вычислений желательно получить длинные числа с большим количеством нулевых битов. Обратите внимание, на картинке p и q представленные в 16-ричной форме, а если 16-ричная цифра равна 0, то все 4 бита этой цифры, также будут равны нулям.
Далее (когда простые числа получены и видны на форме) необходимо щелкнуть кнопку «Генерация ключа»
для автоматического заполнения пустых полей…
Это уже легко и быстро: n (для нахождения остатка по модулю) получаем перемножением p и q.
Функцию Эйлера m тоже без труда получаем перемножением p-1 и q-1.
Открытая экспонента е выбирается большего по возможности размера, но с максимальным количеством нулевых битов
(для скорости возведения в степень). Если текстовое поле для е пустое, то программа сама подберет значение
открытой экспоненты… Но если Вы пожелали ввести в поле для е свое длинное число до щелчка по кнопке «Генерация ключа», то программа его примет по возможности…
А вот закрытую экспоненту d, мультипликативно обратную к числу е по модулю m,
вычисляет специальная функция
CLongRsaNum *Get_d(CLongRsaNum *m_op1, CLongRsaNum *e_op2);
Эта функция входит в модуль ArifmeticRSA.cpp , как и сам класс длинных чисел CLongRsaNum.
Видно, что, получая в виде параметров m и e, функция в результате вернет указатель на длинное число d,
именно, мультипликативно обратное к числу е по модулю m…
В общем, ничего сложного, если модуль длинной арифметики работает безошибочно. Тестируйте…
Кодирование и декодирование по алгоритму RSA
И так, часть вторая:
Процесс RSA кодирования : файл рубится на пакеты заданной длины и вне зависимости,
что находилось в файле (текст, музыка, изображение), каждый пакет рассматривается,
как последовательность бит, а значит как длинное число. Внимание! Кодирование производится
открытым ключом того респондента, кому предназначено послание.
Zp = Op^e mod n – закрытый пакет, длинное число полученное путем взятия остатка
по модулю n от возведения в степень открытой экспоненты е открытого пакета Ор.
Понятно, что длины пакетов Op и Zp будут совпадать.
Только человек, обладающий соответствующим закрытым ключом (d и n) сможет расшифровать пакеты послания.
Декодирование RSA (обратная операция) Ор=Zp^d mod n
Вот поэтому я и говорил, что вторая часть наиболее простая! И кодирование, и декодирование выполняется одной функцией (кодеком)
void Main_codec(unsigned char *pack, int sizpack, CLongRsaNum *de, CLongRsaNum *n);
- Первый параметр – указатель на пакет (открытый или закрытый)
- Второй параметр – размер пакета
- Третий параметр – экспонента (открытая или закрытая)
- Четвертый параметр – модуль для взятия остатка.
Тогда Zp129 = Zp128 * Zp1
Как видите, нам необходимо вычислять сомножители, возводя пакет в степень только тех степеней двойки (27 и 20), где в экспоненте расположены 1. А все нулевые биты можно смело игнорировать… Хочу еще добавить, что возводить пакет в степень степени двойки очень легко. Так…
Zp2 = Zp * Zp;
Zp4 = Zp2 * Zp2;
Zp8 = Zp4 * Zp4 и так далее….
В цикле перемножаем само на себя значение, полученное на предыдущем шаге (на предыдущей итерации)…
Создание цифровой подписи файла, используя алгоритм RSA
И, наконец, третья часть:
Суть цифровой подписи – это гарантия того, что подписанный файл не был изменен с момента создания цифровой подписи автором файла.
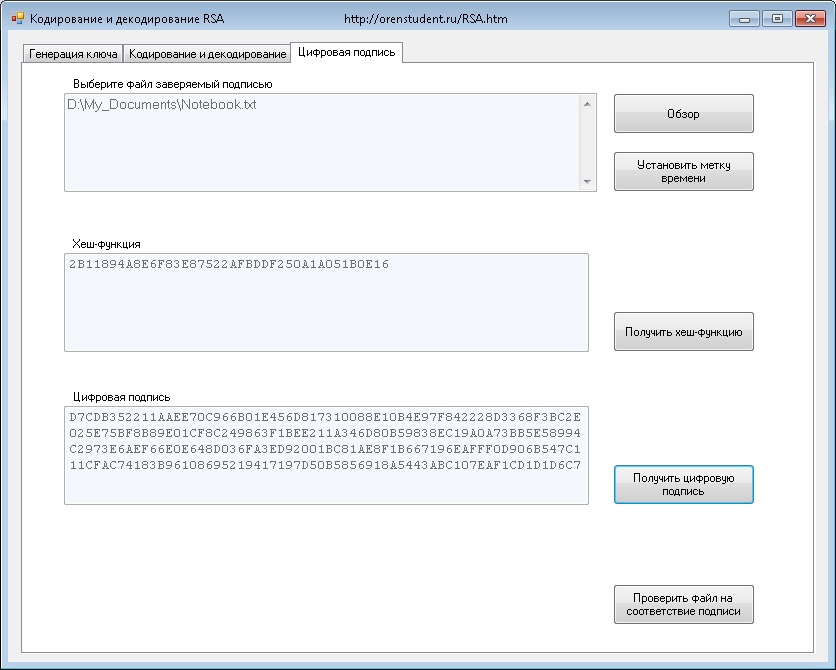
В жизни это выглядит так:
Автор файла с очень важными данными перед его отправкой щелкает кнопку
«Получить цифровую подпись» (что предварительно надо выбрать, т.е. указать сам файл в верхнем окне, Вы догадались? )…
В результате в той же папке создается небольшой файл цифровой подписи с расширением *.dsf (по размеру равен одному пакету). В процессе генерации цифровой подписи используется закрытый ключ автора (d и n). Вот сейчас можно отправлять оба файла респонденту, который имеет открытый ключ автора и может всегда проверить (обнаружить искажения) соответствующего файла.
Как видите, все логично… Подписать документ может только автор (обладатель закрытого ключа), а убедиться что файл не был случайно или злонамеренно искажен, может любой заинтересованный респондент, который имеет открытый (публичный) ключ автора… Повреждение или утеря файла цифровой подписи (*.dsf) ведет к утрате гарантии подлинности данных в документе…
Ну, а сейчас опишу сами процессы генерации цифровой подписи и проверки документа на соответствие цифровой подписи…
Генерации цифровой подписи
Прежде всего, файл хешируется или, другими словами, вычисляется его хеш-функция!
В данной работе требовалось использовать SHA-1 (Secure Hash Algorithm 1 — алгоритм криптографического хеширования),
суть которого прекрасно описана в Рунете. Какого бы большого размера не был исходный файл,
результатом работы SHA-1 будет хеш-функция размером 32 байта (160 бит).
Даже если Вы незначительно измените содержимое файла (добавите один пробел в конце или замените одну маленькую букву на заглавную), новая хеш-функция будет очень сильно отличаться от первоначальной. Подобрать специально два разных текста, которые бы имели одинаковые хеш-функции – задача не из легких…
Если полученную хеш-функцию закрыть секретным ключом автора, то и получится цифровая подпись данного файла. Размер ее всегда будет равен размеру пакета, т.к. берется остаток по модулю n.
Еще раз подчеркиваю, что никто кроме автора не может создать цифровую подпись, но все обладатели открытого ключа автора, могут из цифровой подписи получить хеш-функцию подписанного (начального, не искаженного) файла.
Проверка файла на соответствие подписи
Поскольку SHA-1 является общедоступной, то респондент, желающий убедиться в подлинности файла, хеширует его и сравнивает с хеш-функцией полученной путем декодирования из цифровой подписи… Если совпадают, то файл не изменялся и его данным можно доверять…
Можете протестировать:
создав цифровую подпись, нажмите «Проверить файл на соответствие подписи»…
получите ответ о соответствии. Затем измените файл (сохранив изменения, пусть самые незначительные)
и еще раз нажмите «Проверить файл на соответствие подписи» - ответ уже будет отрицательным.
Обмануть этот механизм, ох как сложно…
скачать exe-файл для тестирования (длина ключа 512 бит)
Другие примеры на тему «Шифрование, Кодирование и/или Сжатие Информации»
Другие примеры на языках «C»,«C++»,«C#»
Поделиться в соц сетях:





