Задачи на тему «Геометрия». Массивы. Консольные приложения на Си, С++.
Часто встречающиеся задачи...
- Окружность через три точки
- Прямая пересекающая окружности
- Параллельность прямых
- Точки на сторонах треугольников
- Площадь выпуклого многоугольника
Их список будет расти...
Окружность через три точки
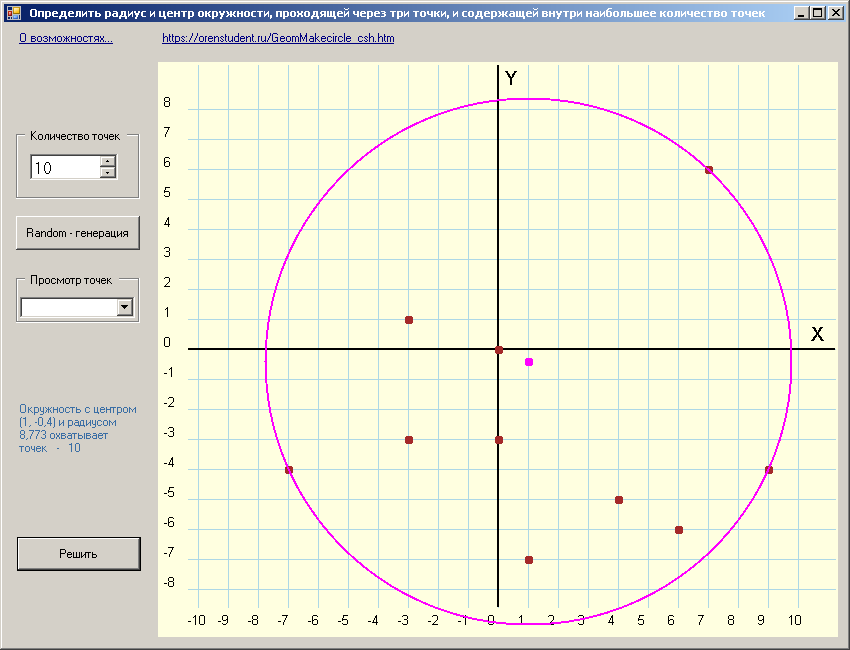
Определить радиус и центр окружности, проходящей, по крайней мере, через три различные точки заданного множества точек на плоскости и содержащей внутри наибольшее количество точек этого множества.
Из школьного курса известно, что через любые три точки (если только они не лежат на одной прямой) можно провести окружность. Строится серединный перпендикуляр для первых двух точек, т.к. центр окружности будет лежать только на нем (обеспечена равноудаленность). А его пересечение со вторым серединным перпендикуляром даст точку - центр окружности, которая будет равноудалена до всех трех заданных точек.
Пусть пользователь задает только количество точек, а их координаты будут генерироваться случайно.
Впрочем, в тестовом варианте, надо дать возможность явно указывать координаты некоторых точек
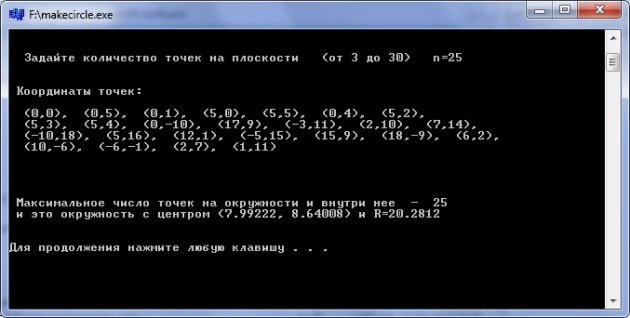
Рис.1 Окружность через три точки
Вот результат, после того как пользователь ввел число 25.
Кому интересно C++, Скачать ехе-файл для тестирования
А здесь C# Скачать ехе-файл для тестирования
Другие примеры на языках «C»,«C++»,«C#»
Прямая пересекающая окружности
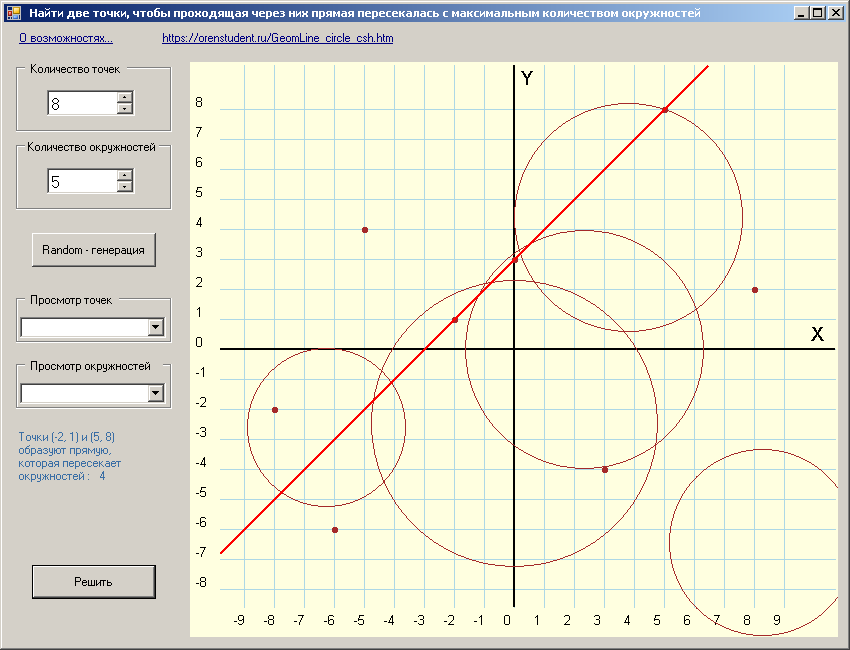
На плоскости заданы множества точек A и множество окружностей B.
Найти две различные точки из A такие, чтобы проходящая через них прямая
пересекалась с максимальным количеством окружностей из B.
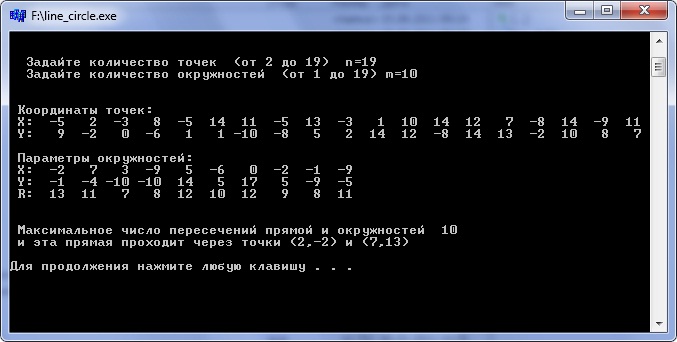
Рис.2 Прямая пересекающая окружности
В цикле по каждым двум точкам находим уравнение прямой.
Затем, во вложенном цикле, определяем расстояние до этой прямой от каждого центра окружности и сравниваем с ее радиусом.
И становится понятно, пересекает прямая окружность или нет
Кому интересно, Скачать ехе-файл для тестирования
Другие примеры на языках «C»,«C++»,«C#»
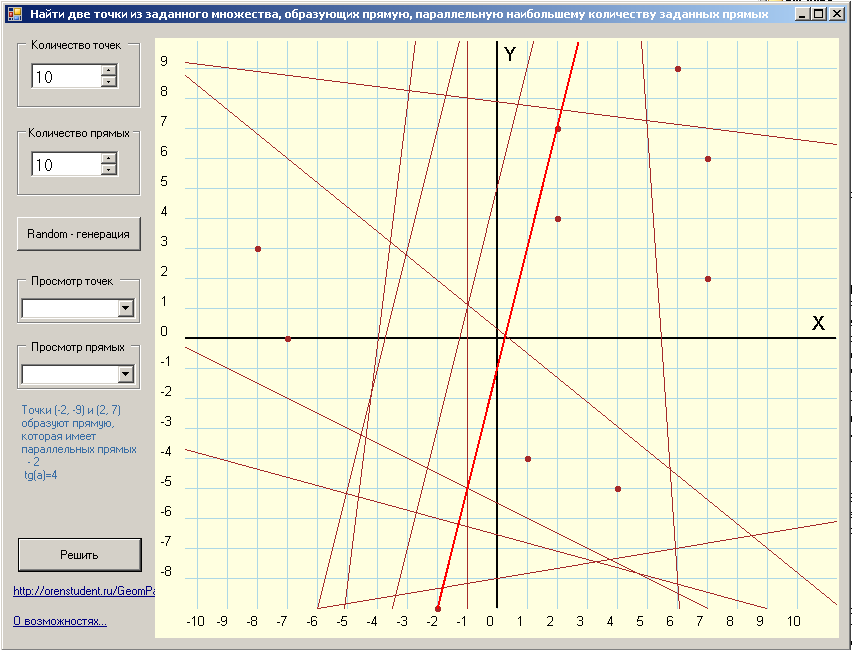
Параллельность прямых
На плоскости задано множество точек А и множество прямых В.
Найти две различные точки из А такие, чтобы проходящая через них прямая была параллельна наибольшему количеству прямых из В.
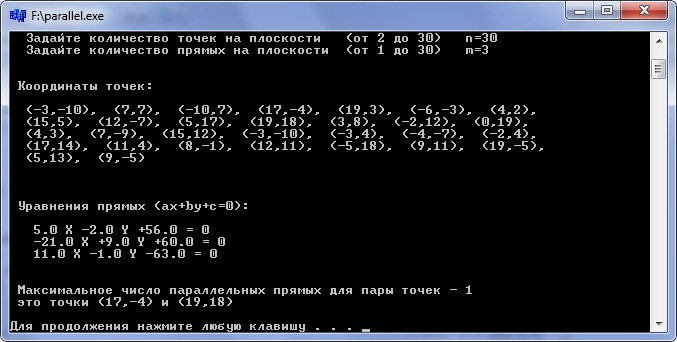
Рис.3 Параллельность прямых
Ну, здесь еще проще: после того как по паре точек определили уравнение прямой остается сравнить коэффициенты наклона полученной прямой со всеми прямыми из множества В.
Кому интересно, Скачать ехе-файл для тестирования
Другие примеры на языках «C»,«C++»,«C#»
Точки на сторонах треугольников
Среди треугольников с вершинами в заданном множестве точек на плоскости указать такой,
стороны которого содержат максимальное число точек заданного множества.
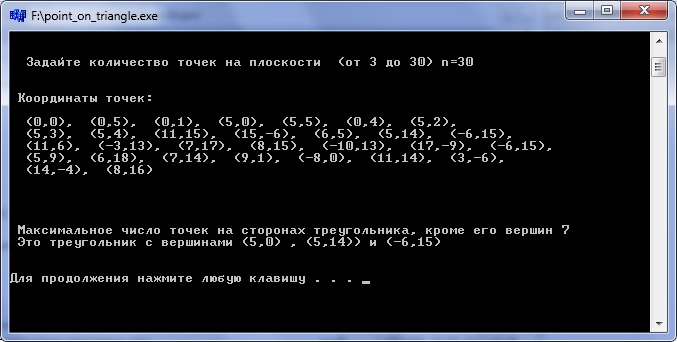
Рис.4 Точки на сторонах треугольников
Определить, лежит ли точка на «прямой» по уравнению прямой задача считай дошкольная
А сравнив координаты вершин треугольника и выбранной точки, можно однозначно сказать, лежит ли она на стороне треугольника или за пределами
Остается подсчитать все это в циклах и запоминать наилучший вариант из просмотренных.
Кому интересно, Скачать ехе-файл для тестирования
Другие примеры на языках «C»,«C++»,«C#»
Площадь выпуклого многоугольника
На координатной плоскости заданы в порядке следования все N вершин выпуклого многоугольника (2 < N < 21). Найти площадь многоугольника или (в противном случае) сообщить, что многоугольник не является выпуклым.
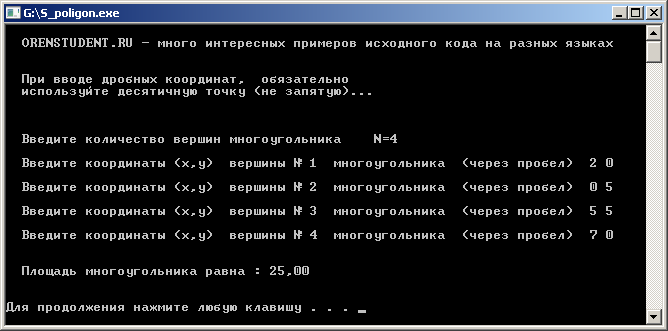
Рис.5 Площадь выпуклого многоугольника
Количество вершин многоугольника можно запросить у пользователя до ввода координат этих вершин
Затем заполнить массив точками (координатами) вершин многоугольника (тоже с участием пользователя)
Остается :
- проверить многоугольник на выпуклость, посылая последовательно по 3 точки в матричный детектор направления поворота;
- разбить выпуклый многоугольник на треугольники;
- сложить площади треугольников, которые тоже легко вычисляются с помощью матричного аппарата.
Весь код главной функции не превышает 30 строк, а три вспомогательные функции не превышают 20 строк...
Кому интересно, Скачать ехе-файл для тестирования
Другие примеры на языках «C»,«C++»,«C#»
И в завершение
Однотипность этих задач видна невооруженным взглядом
Поэтому, структуры данных и многие функции, несущие явную геометрическую направленность,
выделены в отдельный модуль.
Не сомневаюсь, он пригодится мне еще не раз
Да и Вам, наверное, тоже
Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку ...
Поделиться в соц сетях:






