Приведение матрицы к виду верхней треугольной «Алгоритм Барейса»
Матрица - двумерный массив. Это особый тип организации данных, который выступает как единое и неразрывное целое.
- Актуальность Алгоритма Барейса
- Матрицы треугольного вида
- Суть Алгоритма Барейса
- Исходный код VBA EXCEL
Актуальность Алгоритма Барейса
Как и вся матричная арифметика, алгоритм Барейса совершенствует (упрощает) способ обработки данных, находящихся в матрице.
Приведение матрицы к треугольному виду требуется, прежде всего, для решения систем линейных уравнений,
а именно для вычисления определителя матрицы. Ведь самый быстрый способ вычислить определитель — это привести
матрицу к треугольному виду (по алгоритму Гаусса), а затем перемножить её диагональные элементы.
О дополнительных преимуществах алгоритма Барейса сказано ниже…
Матрицы треугольного вида
Название говорит само за себя.
Если все элементы матрицы ниже главной диагонали равны 0, то это верхняя треугольная матрица. Если выше главной диагонали все 0, то это нижняя треугольная матрица.
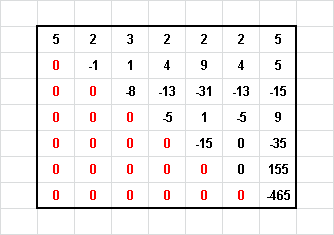
Рис.1 Матрицы треугольного вида
Суть Алгоритма Барейса
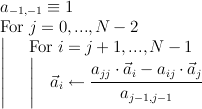
Рис.2 Суть Алгоритма Барейса
Изучив преимущества и недостатки имеющихся алгоритмов (Гаусса и Барейса), я остановился на алгоритме Барейса, так как:
- если матрица состоит из целых чисел, алгоритм Барейса позволяет привести её к треугольному виду с использованием только целочисленной арифметики;
- определитель исходной матрицы равен правому нижнему элементу матрицы, полученной в результате алгоритма Барейса, т.е. не нужно выполнять перемножение элементов главной диагонали, как после алгоритма Гаусса;
- алгоритм Барейса так же, как и алгоритм Гаусса, может быть улучшен путём добавления перестановки строк, но в нашей задаче это излишне;
Поэтому код VBA приведения будет следующим:
For j = 1 To n - 1
jj = mR.Cells(j, j) 'определяем первый множитель
If j = 1 Then 'определяем знаменатель
znm = 1
Else
znm = mR.Cells(j - 1, j - 1)
If znm = 0 Then Exit Function
End If
For i = j + 1 To n
ij = mR.Cells(i, j) 'определяем второй множитель
For k = j To n
mR.Cells(i, k) = (jj * mR.Cells(i, k) - ij * mR.Cells(j, k)) / znm
Next k
Next i
Next j
Где mR as Range – переменная модуля, ссылающаяся на выделенная область.
j- индексы строк, а i- индексы столбцов выделенной области.
Ячейка, обозначенная как а-1,-1 лежит вне области выделения
(т.е. выше и левее ячейки а0,0 ) и ей в начальный период обязательно присваивается 1.
В своей функции вместо а-1,-1 я использую переменную znm (от знаменатель) и базовое
значение счетчиков 1 вместо 0. Суть алгоритма это не меняет. При пошаговом выполнении
программы прекрасно прослеживается постепенное приведение матрицы к верхнему треугольному виду.
Исходный код VBA EXCEL
Для работы с матрицами в Microsoft EXCEL существует три функции листа Excel.
Это:
- МОПРЕД(массив) - возвращает определитель матрицы (матрица хранится в массиве);
- МОБР(массив) - возвращает обратную матрицу для матрицы, хранящейся в массиве;
- МУМНОЖ(массив1;массив2) - возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2;
Первую из этих функций буду использовать для проверки результата.
Кроме того:
- в макросе проводится проверка на соответствие выделенной области, и если размеры не совпадают (а матрица должна быть квадратной), то выдается сообщение и работа макроса завершается;
- в ячейку AJ2 вводится формула для вычисления определителя (на основе функции МОПРЕД) выделенной области; (просто для проверки)
- в завершающем сообщении предлагается очистить лист «Результат» по желанию пользователя;
скачать xlsm-файл для тестирования
Другие примеры на языке «Visual Basic for application (VBA)»
Другие примеры на тему «Матрицы и операции вычислений с ними»
Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку ...






