Метод пятиточечной прогонки. Решение Дифференциальных уравнений. Разностные схемы
Решение краевой задачи дифференциального уравнения сеточными методами высокого порядка точности - программа, тестирующая метод пятиточечной прогонки, для решения системы уравнений, построенной с помощью разностных схем на Delphi.
Постановка задачи:
Дифференциальная задача:
y''(x)=f(x,y(x));
f – заданная функция
K – число отрезков разбиения (узлов сетки), задается с клавиатуры.
[a,b] – рассматриваемый промежуток, задается с клавиатуры.
y(0) = φ, y(K)=ψ - краевые условия;
Используя заданную схему сеточной аппроксимации, решить систему сеточных уравнений методом пятиточечной прогонки.
Заданная схема сеточной аппроксимации:
Для внутренних точек

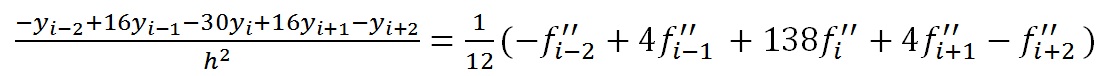
Для первого уравнения (i=1) предлагается
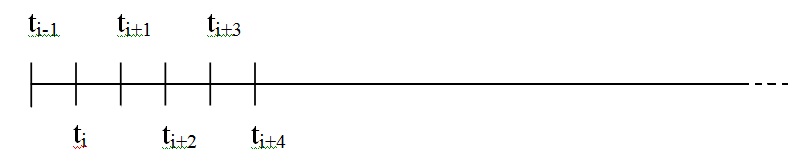
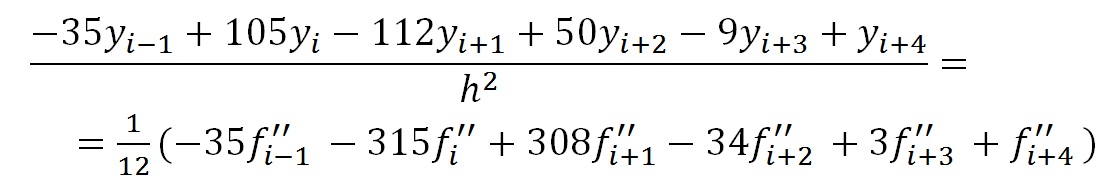
Для последнего уравнения (i=k-1) предлагается

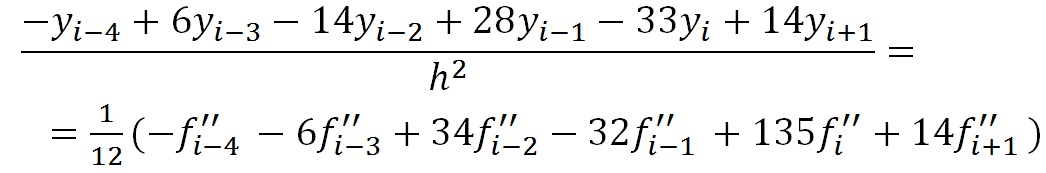
Решение:
Понятно, что пятиточечная прогонка несколько сложнее трехточечной, и ее использование целесообразно только в случаях, требующих повышенной точности результата.
Тестирование метода пятиточечной прогонки я решил продемонстрировать на примере 4 функций (разумеется, сначала брал решение, потом его дифференцировал и получал F(x))
F(x) = 2Sin(x) + 4xCos(x) – y(x); //решением будет y= x2Sin(x) +C
F(x)= 6x*ln(x) + 5x; //решением будет y= x3ln(x)+C
F(x):= – Cos(x); //решением будет y= Cos(x)+C
F(x):= 0; (без кривизны) //решением будет y= K*x + C
Поскольку я знаю формулы решения, то могу строить теоретически правильные графики для сравнения.
Задача, конечно, не тривиальна. Используются одновременно три разностных схемы.
Коэффициенты для каждой из них будут свои, и рассчитывать их надо аккуратно…
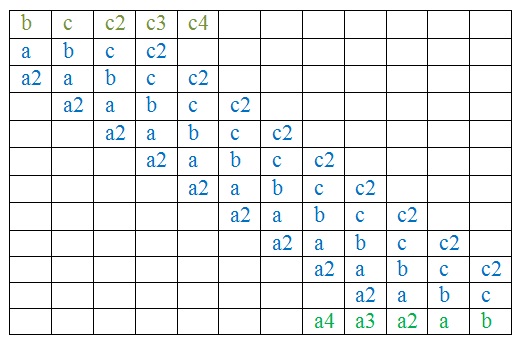
Получилась такая разряженная матрица (в пустых клетках, конечно, нули).
Сначала в массив y[i] помещаем значения F(x,y,y’) как вектор свободных членов…
Далее, методом пятиточечной прогонки (преобразованиями Гаусса) приводим эту матрицу к единичной, и в результате в векторе-столбце F(x,y,y’) , а значит и в массиве y[i] получаем искомые у(х[i]) для каждого узла сетки.
Полученный массив остается вывести на график и в текстовое окно результата.
Ну, и сравнить с эталонной функцией…
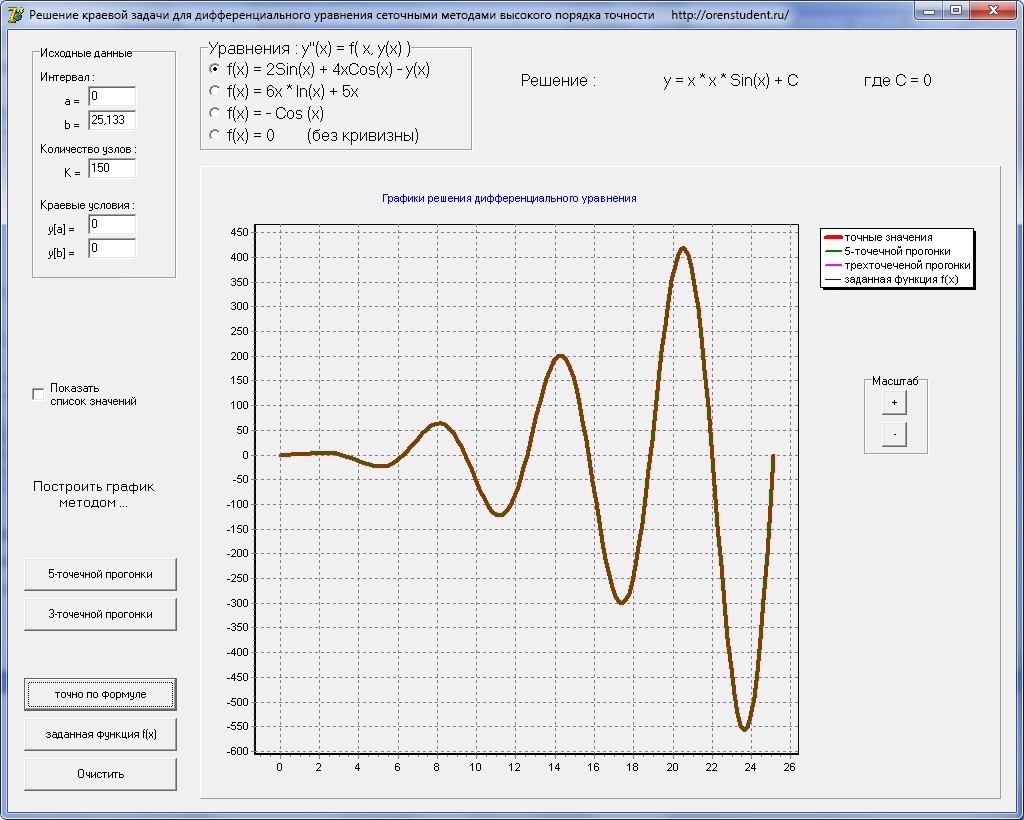
Вот как классно совпадает график рассчитанный с теоретическим (точным)…
Приобретайте код и тестируйте на своих функциях…
Или я могу ваши функции поместить в код…
Другие примеры на тему «РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»
Другие примеры на языке «Delphi»
Поделиться в соц сетях:





