Определить радиус и центр окружности, содержащей наибольшее количество точек множества
Продолжая тему "Геометрия"…
- Формулировка задания: Определить радиус и центр окружности
- Построение окружности через три точки
- Перебор множеств точек
- Визуальное представление на Координатной плоскости
- Случайная генерация множест точек
- Исходный код на C#
С визуальным представлением на координатной плоскости
Формулировка задания: Определить радиус и центр окружности
Определить радиус и центр окружности, проходящей, по крайней мере, через три различные точки заданного множества точек на плоскости и содержащей внутри наибольшее количество точек этого множества.
Пусть пользователь задает только количество точек, а их координаты будут генерироваться случайно.
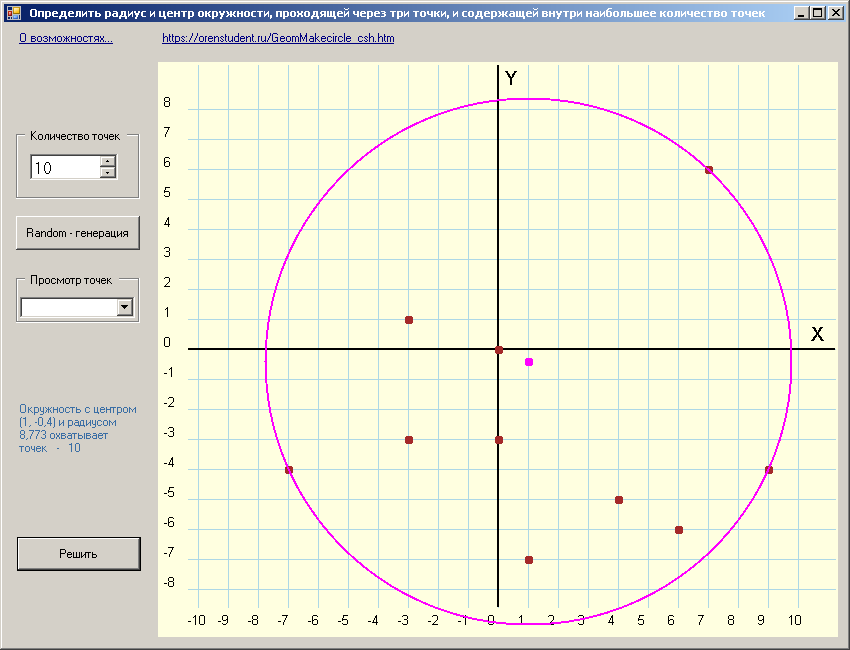
Рис.1 Формулировка задания: Определить радиус и центр окружности
Поскольку нет ограничение на величину «Радиуса», то всегда найдутся такие три точки, окружность через которые охватит все точки заданного множества.
Построение окружности через три точки
Известно, что через любые три точки (если только они не лежат на одной прямой) можно провести окружность.
Строится серединный перпендикуляр для отрезка, образованного первыми двумя точками, т.к.
центр окружности будет лежать только на нем (обеспечена равноудаленность).
А его пересечение со вторым серединным перпендикуляром даст точку - центр окружности,
которая будет равноудалена до всех трех заданных точек.
Перебор множеств точек
Перебор точек из заданного множества следует выполнять в трех циклах, так как каждая тройка точек (если они не лежат на одной прямой) позволяет построить уникальную окружность.
Окружность tmpCircle по трем точкам будет определена, если найдены ее параметры - это Радиус и Центр.
Для определения вхождения любой точки множества в пределы этой окружности, необходимо сравнить R (радиус) окружности tmpCircle и расстояние от центра окружности до каждой точки из множества.
Визуальное представление на Координатной плоскости
Координатная плоскость (из школькой программы) и координатная плоскость формы Windows (c её параметрами left, top в пикселях) отличаются друг от друга (направлением оси ОУ), но математическими преобразованиями всегда можно связать любые две координатные системы отсчета.
Т.е. необходимо решить подзадачу: из имеющихся координат любой точки в системе_1, получить координаты этой же точки в системе_2.
В программном коде это решение представлено. Тестируйте…
Случайная генерация множест точек
Чтобы не утруждать пользователя вводом координат - множество точек генерируются случайным образом.
//------------------------------
const int bottomLim = -9, topLim = 10; //пределы генерации случайных чисел
siz1 = (int)numericUpDown1.Value; //размер массива
arrPoints = new Point[siz1]; //cоздается массив нужного размера для хранения точек
Random rnd = new Random();
for (int i = 0; i < siz1; i++) //здесь заполнить массив точек
{
arrPoints[i] = new Point(rnd.Next(bottomLim, topLim), rnd.Next(bottomLim, topLim));
}
//------------------------------
Исходный код на C#
Данный код написан на Visual Studio 2012, но для всех старших версий проблем с открытием быть не должно.
В крайнем случае, свяжемся и все проблемы решим…
скачать ехе-файл для тестирования
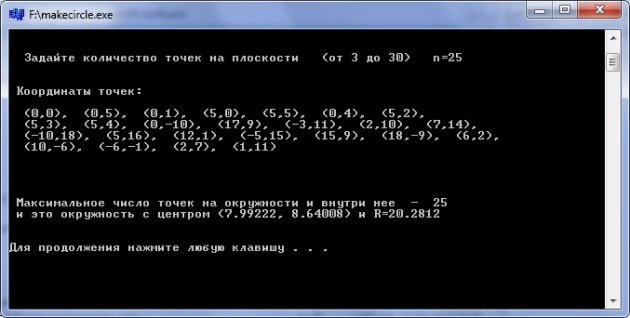
Другие примеры на языках «C»,«C++»
Другие примеры на тему «Математические методы компьютерной 2D 3D графики»
Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку ...
Поделиться в соц сетях:






